海轰Pro
温馨提示
MML：Mathematics for Machine Learning
若移动端查看数学公式不全或显示错误
可以「复制文章链接至PC端」进行查看
3.1 矩阵的初等变换
定义
矩阵的初等「行」变换
对调两行（对调i，j两行，记作） 以数乘某一行中的所有元素（第i行乘以k，记作） 把某一行所有的元素的k倍加到另一行对应的元素上（第j行的k倍加到第i行上，记作）
「列」变换同理，对列进行相应的操作（也是上面三种操作）
初等行变换、列变换统称初等变换。如果矩阵A经过有限次初等「行变换」变成B，就称矩阵A与B行等价，记作
如果矩阵A经过有限次初等「列变换」变成B，就称矩阵A与B列等价，记作
如果矩阵A经过有限次初等变换变成矩阵B，那么称「矩阵A与B等价」，记作
注：
❝后文中使用如下符号代表行、列变换
❞
等价具有的性质
矩阵之间的等价关系具有以下性质：
反身性 对称性 若，则 传递性 若，则
矩阵类型
1、行阶梯形矩阵
❝可以画出一条阶梯线，「线的下方全为0」；
每一个台阶只有一行，台阶数即是非零行的行数，阶梯线的「竖线后面的第一个元素为非零」元，也就是非零行的第一个非零元。
❞
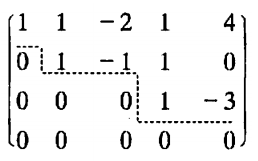
2、行最简形矩阵
❝在行阶梯形矩阵定义的基础之上还要求：
❞
「非零行的第一个非零元为1」
且这些「非零元所处的列的其他元素为0.」
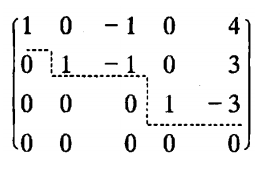
任何矩阵总可经过有限次初等变换将其变为行阶梯形矩阵、行最简形矩阵。
3、标准形矩阵
❝对行最简形矩阵再进行处等列变换，可以得到一种形状更简单的矩阵，成为标准形矩阵。
其特点是左上角是一个单位矩阵，其余元素均为0.
❞
对于矩阵A，总可以经过一系列初等变换转化为标准形矩阵F
其中r为行阶梯形矩阵中非零行的行数。
4、初等矩阵
❝由「单位矩阵」E经过「一次」初等变换得到的矩阵称为初等矩阵
❞
有三种初等变换，则有三种初等矩阵，下面以行初等变换为例
（1）将单位矩阵中的第i、j行对调，得初等矩阵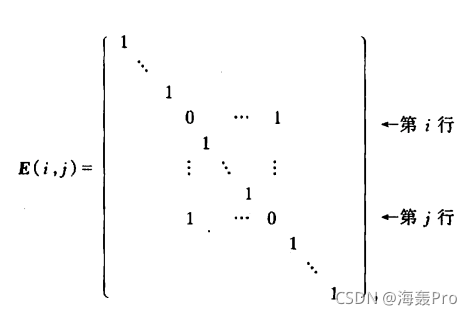
用m阶初等矩阵左乘矩阵A，其中，得到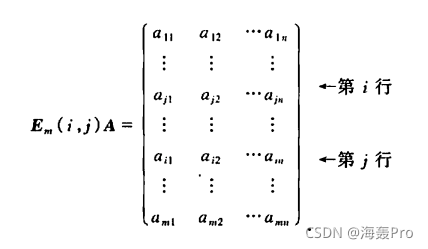
观察结果，可以发现最终结果其实就是「将A矩阵中第i、j行进行了对调」
举个实际例子（「左乘」）：
对调单位矩阵的第1、3行
同理，以n阶初等矩阵「右乘」矩阵A，结果就是相对于对矩阵A进行列变换
（2）以数乘单位矩阵的第i行（或第i列），得到初等矩阵
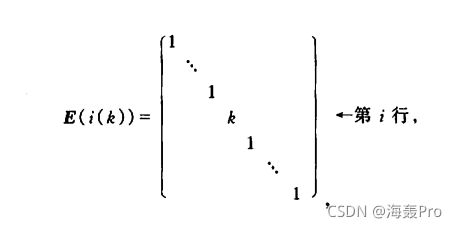
可以发现，矩阵「左乘矩阵A，结果就是相对于数k乘以A的第i行」
举个实际例子（「左乘」）：
单位矩阵第二行乘以k=2
同理，「右乘A，相当于k乘以A的第i列」
（3）以k乘E的第j行加到第i行（或k乘以第j列加到第i列），得到初等矩阵
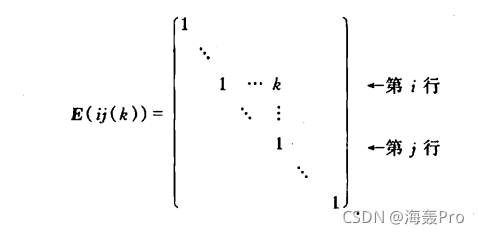
左乘时，相当于把矩阵A的第j行乘k加到第i行上
举个实际例子（「左乘」）：
单位矩阵第3行乘以k=2加到第2行上
同理，右乘时，相当于把矩阵A的第j列乘k加到第i列上
性质
从上面的讨论中，可以得出
性质1
设A是一个m*n矩阵
对A施加一次初等「行」变换，相当于在A的「左边乘以」相应的「m阶」初等矩阵； 对A施加一次初等「列」变换，相当于在A的「右边乘以」相应的「n阶」初等矩阵
初等矩阵都是可逆的，且其逆矩阵都是同一类型的初等矩阵
注意
「实例演示」
设3阶单位阵E
很显然
(E)E=E E(E)=E
所以单位阵的逆矩阵为其本身 即
假设对E的第二行乘以2
得到
那么
有
假设对E的第3行乘以2 再加到第2行上
得到
那么
有
性质2
方阵A可逆的充分必要条件是存在有限个初等矩阵使得
证明：
「先证明充分性：」
设
因为初等矩阵可逆，有限个可逆矩阵的乘积依然可逆
所以A可逆
「证必要性：」
假设n阶方阵A可逆
A通过一系列变换转换为标准形矩阵F
那么F也可以通过一系列初等变换转换为A
所以
因为A可逆，也可逆
所以F也可逆
又因为
若$r
那么 说明F不可逆 与前提条件相反
所以
即）
所以
定理1
设A、B均为m×n矩阵，那么
【指对A进行初等行变换】的充分必要条件是存在m阶可逆矩阵P，使得 【指对A进行初等列变换】的充分必要条件是存在n阶可逆矩阵Q，使得 的充分必要条件是存在m阶可逆矩阵P、n阶可逆矩阵Q，使得
推论
方阵A可逆的条件是
「证明充分性：」
因为
所以存在初等矩阵P，使得
因为
那么一定可逆
「证明必要性：」
首先通过初等行变换一定可以变为
若$r
因为可逆 所以F可逆
若 则不可逆
所以
那么
即
故
补充
定理1表明，如果，即A经过一系列初等行变换可以变为B，则一定存在可逆矩阵P，使得，那么如何求P呢？
假设已知A、B的情况下
首先依据题意可得
所以
推出
矩阵(A,E)通过初等行变换可以变为矩阵(B,P)
A、E、B已知，那么P就一目了然啦
注意：
矩阵(A,E)的意思是矩阵A与矩阵E横行拼接
比如
那么矩阵
当B=E时，此时求的P就是A的逆矩阵（求逆矩阵的一个常用方法！）
结语
文章仅作为学习笔记，记录从0到1的一个过程
希望对您有所帮助，如有错误欢迎小伙伴指正～
