温馨提示

MML：Mathematics for Machine Learning

若移动端查看数学公式不全或显示错误

可以「复制文章链接至PC端」进行查看

4.1 向量组及其线性组合

定义1

1. n维向量

定义：n个有次序的数所组成的数组，其中这n个数成为该向量的n个分量，第i个数称为第i个分量

2. 实向量

定义：向量中的所有的分量均为实数

3. 复向量

定义：向量中至少有一个分量为复数

4. n维列向量a

5. n维行向量b

❝

一般来说，列向量用黑体小写字母等表示，行向量用等表示

无特殊说明时，一般看作为「列向量」

❞

6.  三维向量空间

定义：三维向量的全体所组成的集合

称为三维向量空间

在讨论向量的运算时，将向量看作有向线段

在讨论向量集合时，则把向量r看作以r为「向径」的点P，从而把点P的轨迹作为向量集的图形

❝

向径：一般指位置矢量。在某一时刻，以坐标原点为起点，以运动质点所在位置为终点的有向线段

❞

例如点集 是一个平面（a、b、c不全为0）

❝

假设a = b = c = 1 d = 0

则为 x + y + z = 0

稍微变形一下 z = - x - y

这样就容易看出其是一个平面了

❞

于是向量集

也叫做向量空间中的平面，并把作为它的图形

7.  n维向量空间

n维向量的全部所组成的集合

❝

其中n维向量的集合

叫做n维向量空间

❞

8.  向量组

定义：若干个同维数的列向量（或同维数的行向量）所组成的集合

❝

一个 m * n 矩阵的全体列向量 是一个含有 「n个」 「m维列向量」的向量组

全体行向量是一个含 m个 n维行向量的向量组

❞

矩阵的列向量组和行向量组都是只含 「有限」个向量 的向量组；反之，一个含有限个向量组总可以构成一个矩阵

比如，m个n维列向量所组成的向量组可以构成一个n * m 矩阵

m个n维行向量所组成的向量构成一个m * n 矩阵

注：为列向量

总之，含有有限个向量的有序向量组可以与矩阵一一对应

定义2

（1）给定向量组，对于任何一组实数，表达式称为向量组A的一个线性组合，称为这个线性组合的系数

（2）给定向量组和向量b，如果存在一组数，使得

（3）则向量b是向量组A的线性表示，也就是说方程组有解

定理1

向量能由向量线性表示的充分必要条件是矩阵的秩等于矩阵的秩

❝

其实就是方程组有解 因为线性方程组有解，充分必要条件是（上一章的定理5）

❞

定义3

设有两个向量组及，若B组中的每个向量都能由向量组A线性表示，则称向量组B能由向量组A线性表示。

❝

若向量组A与向量组B互相线性表示，则称这「两个向量组等价」

❞

设向量组，向量组

若能由线性表示 那么对每个向量

存在数，使得

从而得到

进而

其中矩阵则称为这一线性表示的「系数矩阵」

上面向量组A、B都是使用列向量组进行组合的，现在来讨论为「行向量」组来组成A、B

设

因为B中的任意一条向量都可以用线性表示

那么有

进而得到

推出

由以上可知，若，则矩阵C的列向量组都能由矩阵A的列向量组线性表示，B则为这一表示的系数矩阵

❝

对应上式中的，对应，那么就对应

❞

同时，若C的行向量组都可以由B的行向量组线性表示，那么A就为这一表示的系数矩阵

❝

利用 对应这里的 得到 A就是系数矩阵

❞

定理2

向量组能由向量组线性表示的充分必要条件是矩阵的秩等于矩阵的秩，即

「说明」

因为可以由进行线性表示

那么就存在一个系数矩阵，使得

也就可以说

至少存在一个解

又因为

线性方程组有解的充分必要条件是

所以

推论

向量组与向量组等价的充分必要条件是

其中，A和B是向量组A和B所构成的矩阵

「证明」：

因为可以由进行线性表示，那么由定理2可以得

同理，也可以由进行线性表示，那么一样有

又因为

得到

证明完成！

举例

例 1

设

证明向量能由向量组线性表示，并求出表达式

「证明：」

设

由定理1可知 向量b若能由向量组线性表示

则

这里我们只需要对进行化简，求秩（求的同时，也就一目了然了）

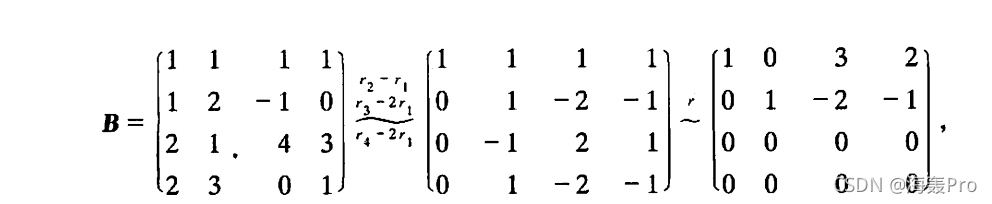由

可得

移项，得

令 得

推出

❝

注：

❞

所以

，其中c可以取任何值

例2

设

证明向量组与向量组等价

证明：

设

由「定理2的推论」 可知 与等价

说明

对进行化简

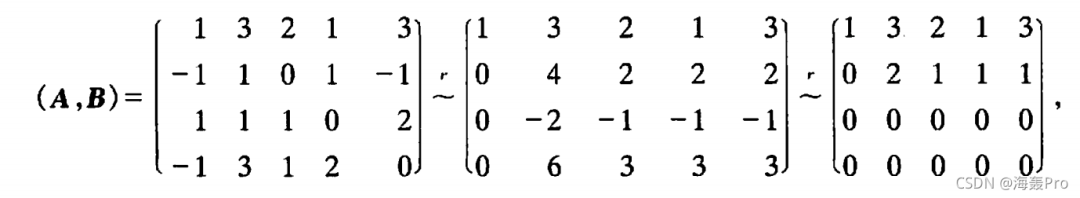得到

又可以明显的看出来中有不等于0的2阶子式

说明

又因为

所以有

推出

综上

所以与等价

定理3

设向量组 能由向量组线性表示，则

「证明：」

令，

因为可以由线性表示

那么就有

又因为

所以

小结

由上面的定律、推论可得

向量组能由向量组线性表示有矩阵，使得方程有解

结语

文章仅作为学习笔记，记录从0到1的一个过程

希望对您有所帮助，如有错误欢迎小伙伴指正～