等风来也等你
图的遍历是指从图中的某个顶点（该
顶点
也
可称为起始点
）出发，按照
某个
特定
的
方式访问图中的各个顶点，使每个可访问到的顶点都被访问一次。图
的
遍历
方式有两种，
一种
是深度优先遍历
（也
叫作深度优先搜索
，简称
为
DFS）
，还有一种是广度优先遍历
（也叫做
广度优先搜索
，
简称为
BFS）
。
说明：
起始点可以
任意指定，
起始点
不同得到的
遍历
序列也不
相同。
注意：
在遍历
时，每个顶点只能访问一次，
不可
重复访问。
深度优先 遍历 算法
深度优先遍历算法 是经典的图论算法。 它 的 思想 是 ：从一条路径的起始点开始追溯，直到到达路径 的 最后一个顶点，然后回溯，继续追溯下一条路径，直到到达最后的顶点，如此往复，直到没有路径为止。它 的遍历过程如下： （1）以 图中的任一顶点 v 为出发点， 首先访问顶点 v ，并 将其标记为已被访问。 （2）从顶点v的任一个邻接点出发 继续 进行 深度优先的搜索 ，直至图中所有和顶点v连通的顶点都已被访问。 （3）若此时图中仍有未被访问的顶点，则选择一个未被访问的顶点作为新的出发点重复上述过程，直至图中所有顶点都已被访问为止。 这种 图的 遍历 方法应用了堆栈这种数据结构的特点。下面 以 图 12. 4 所示 的 无向图 为例来介绍 这个 方法的遍历过程。
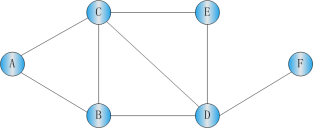
图12 . 4 无向图
第一步 ： 假设 以顶点 A为 起点，将顶点 A压入 堆栈 ， 如图 12. 5所示。
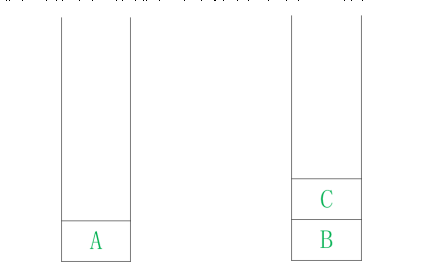
图12 . 5 堆栈图1 图12 . 6 堆栈图 2
第二步 ： 弹出 顶点 A ，将 顶点A的邻接点 B 和 C 压入 堆栈 ， 如图 12. 6所示。 第三步 ： 根据堆栈“后进先出”的 原则， 弹出 顶点C，将 与顶点 C 相邻 并且未 被 访问过的顶点B 、 顶点 D和 顶点 E压入 堆栈 ， 如图 12. 7所示。
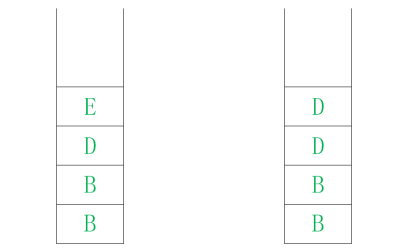
图12 . 7 堆栈图3 图12 . 8 堆栈图 4
第四步 ： 弹出 顶点E，将 与顶点 E 相邻 并且未 被 访问过的顶点D 压入 堆栈 ， 如图 12. 8所示。 第五步 ： 弹出 顶点D，将 与顶点 D 相邻 并且未 被 访问过的顶点B 和 顶点 F压入 堆栈 ， 如图 12. 9所示。
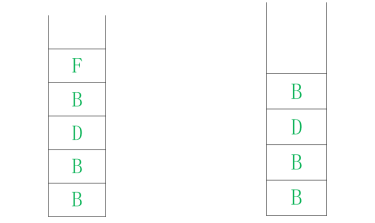
图12 . 9 堆栈图 5 图12 . 10 堆栈图 6
第六步 ： 弹出 顶点F，将 与顶点 F 相邻 并且未 被 访问过的顶点 压入 堆栈 。 由于 顶点F的 邻接点 D 已被访问过，所以无须压入堆栈 ， 如图 12. 10所示。 第七步 ： 弹出 顶点B，将 与顶点 B 相邻 并且未 被 访问过的顶点 压入 堆栈 。 由于 顶点 B 的 邻接点 都 已被访问过，所以无须压入堆栈 ， 如图 12. 11所示。
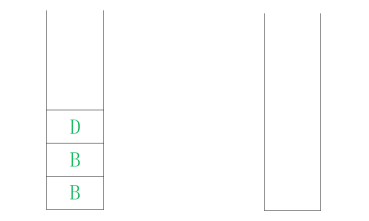
图12 . 11 堆栈图 7 图12 . 12 堆栈图 8
第八步 ： 将堆栈 中的 顶点 依次弹出，并判断是否已经访问过，直到 堆栈 中无顶点可以访问为止 ， 如图 12. 12所示。 由此可知 ，对图 12. 4 中 的图 进行深度 优先遍历 的 顺序为： 顶点A、顶点 C 、顶点 E 、顶点 D 、顶点 F 、顶点 B 。 该 例中应用的深度优先函数的算法如下：
01 def dfs(graph, start):
02 stack = [] #定义堆栈
03 stack.append(start) #将起始顶点压入堆栈
04 visited = set() #定义集合
05 while stack:
06 vertex = stack.pop() #弹出栈顶元素
07 if vertex not in visited: #如果该顶点未被访问过
08 visited.add(vertex) #将该顶点放入已访问集合
09 print(vertex,end = ' ') #打印深度优先遍历的顶点
10 for w in graph[vertex]: #遍历相邻的顶点
11 if w not in visited: #如果该顶点未被访问过
12 stack.append(w) #把顶点压入堆栈
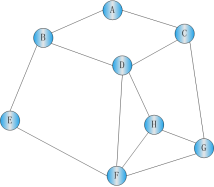
图12 . 13 无向图
代码如下：
01 graph = { #定义图的字典
13 "A": ["B","C"],
14 "B": ["A","D","E"],
15 "C": ["A","D","G"],
16 "D": ["B","C","F","H"],
17 "E": ["B","F"],
18 "F": ["D","E","G","H"],
19 "G": ["C","F","H"],
20 "H": ["D","F","G"],
21 }
22 def dfs(graph, start):
23 stack = [] #定义堆栈
24 stack.append(start) #将起始顶点压入堆栈
25 visited = set() #定义集合
26 while stack:
27 vertex = stack.pop() #弹出栈顶元素
28 if vertex not in visited: #如果该顶点未被访问过
29 visited.add(vertex) #将该顶点放入已访问集合
30 print(vertex,end = ' ') #打印深度优先遍历的顶点
31 for w in graph[vertex]: #遍历相邻的顶点
32 if w not in visited: #如果该顶点未被访问过
33 stack.append(w) #把顶点压入堆栈
34 print("图中各顶点的邻接点：")
35 for key,value in graph.items(): #遍历图的字典
36 print("顶点",key,"=>",end=" ") #打印顶点
37 for v in value: #遍历顶点的邻接点
38 print(v,end=" ") #打印顶点的邻接点
39 print()
40 print("深度优先遍历的顶点：")
41 dfs(graph,"A") #调用函数并设置起点为A
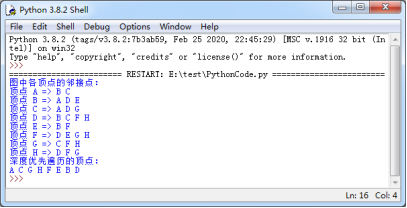
图 1 2 . 14 打印深度 优先遍历序列
