BTNs是怎么玩转生成即压缩的?详解结合贝叶斯统计和深度学习的生成模型 — Bayesian Flow Networks(一)

极市导读
生成即压缩?手把手带各位吃透Bayesian Flow Networks(BFNs)这篇工作,本篇先从BFN的背景、motivation和优势进行介绍,并对其数学框架进行解析。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
前言
前段时间,CW 不小心逛到了一篇好玩的 paper:Bayesian Flow Networks(BFNs),咋一看标题中出现了贝叶斯爸爸的名字,就 feel 到这篇 paper 的数学功力应该不浅,自然也就激发了我这小菜鸟的兴趣。另外还了解到作者是 Alex Graves,他于 2006 年提出的 CTC loss 是语音识别领域的网红。在多伦多大学的博士后时期,他还抱过 Hinton(对!就是那位深度学习三巨佬之一) 的大腿,作者的这种背景也给我增加了信心——这应该是一篇值得一读的 paper。
当时心痒痒的,于是就偷偷扫了下 introduction 部分,发现作者还很会蹭热度——前段时间 OpenAI 提出“压缩即智能”的观点在圈内非常火爆,而在这篇 paper 中,作者也类似地提出一种看待生成模型的通用视角,可谓“生成即压缩”。哈,这令我感觉更有意思了,最终就下定决心在此就这篇 paper 的内容来和大家吹吹水~
但是,这篇 paper 不太好读,内容不少并且数学公式和推导巨多,而且其中许多部分作者大大也没有给出详细的推导过程(可能大神觉得理所当然的东西我这种中庸之辈却很难看透),如果你信心满满地去读很可能会大遭打击(当然,大神请绕开,见笑了~).. 因此,CW 会以一个系列的形式(而非单篇文章)来解析 BFN,尽最大努力为各位朋友打辅助,从而令大家以更低的成本来理解这篇 paper,进而认识到其 idea 中值得借鉴的地方(见仁见智)。
本文是系列中的第一篇,主要对 BFN 的背景、motivation 和 优势 进行介绍,并对其 数学框架 进行解析,以让大家对 BFN 有一个感性(及些许理性)和整体的认识。在后续文章中,CW 会进一步解析 BFN 在面对连续(continuous)数据、离散化(discretised)数据 以及 离散(discrete)数据 时的具体实现,在此建议各位按顺序阅读(当然,调皮鬼请随意~)。
来~ 现在就正式开启这一段漫长之旅吧!

启航:BFN 简介
CW 先向大家稍微介绍下本文的主角——BFN:
这货和其它模型最大的不同在于其输入不是数据(数据集中的样本),而是数据所服从的分布参数!而该分布是人为预设的先验。在训练过程中,根据 贝叶斯推断(Bayesian inference) 方法,不断利用观测样本来更新先验。
但是,仅使用贝叶斯推断会无法整合上下文信息——因为先验是假设多维数据的所有分量都是相互独立的,而贝叶斯更新过程又是独立对每个分量进行。于是,BFN 会利用输入的先验,进一步输出另一个分布,以此作为数据分布的估计,最终生成的样本就是从该分布中采样出来的。BFN 在其中起到了探索上下文信息的作用。
采样生成的过程会先从一个先验开始,将先验参数输入 BFN 后输出另一个分布,从该分布中采样并对样本进行一些处理(具体操作待后文说明),然后将其作为观测样本来更新先验,接着再把校正后的先验继续喂给 BFN 从而更新它的输出分布,就这样不断更新这两个分布。待一定步骤后,才把从 BFN 的输出分布中采样出来的结果作为最终生成的样本,有点类似于 扩散模型(diffusion models) 的去噪生成过程。
对于 BFN 来说,这种搞法有点像“自己更新自己”:我的输出更新我的输入,我的输入又反过来更新我的输出.. 不断重复这个过程,就看谁先累趴,有点可爱~

BFN 最大的优势在于其输入是连续、可微分的:尽管对于离散型数据,由于网络的输入始终是数据分布的参数,因此天然地位于 probability simplex(概率单纯形) 上,从而具有原生的可微性,无需做各种约束来适配(比如如何将离散点空间映射到连续可微的光滑曲线上),能够直接优化数据的似然函数。
这也为基于梯度指导的采样生成和少步生成提供了可能。而利用梯度信息来指导采样过程能够更快地找到高概率区域,从而提高采样效率和质量。
综合来说,BFN 对于无论是对于连续数据(continuous data),离散化数据(discretised data) 亦或是 离散数据(discrete data) 都得心应手,能够天然地适配不同类型的数据与分布。
以宏观角度来看,BFN 结合了传统统计学与深度学习的优势,前者通过贝叶斯推断来体现,在数学上提供了保障性与可解释性;而后者则利用了神经网络的玄学能力——能够对高维空间中变量之间的复杂交互关系进行有效建模。
一场游戏:生成即压缩
作者认为,使用深度神经网络的现代生成模型是通过对图像所有像素的联合分布进行建模来生成高分辨率图像的,这些模型包括:autoregressive models, flow-based models, deep VAEs & diffusion models,它们成功的关键在于将联合分布的编码过程“分解”为一系列的步骤,从而避免了“维度灾难”——在高维度情况下,所有变量之间的直接交互会变得十分复杂和可怕。
虽然在细节上,以上模型的做法不尽相同,但一种通用视角是将它们建模的过程均看作是“最优比特传输问题”:消息传输者(sender) 向 消息接收者(receiver) 传输多轮(经过编码的)消息(message),这些消息携带了数据(data)的信息。在每一轮收到消息前,receiver 会对消息进行猜测;待收到消息后,他就会利用获得的信息来更新“猜测策略”,以便后续猜得更准。在这个过程中,loss 函数定义为传输所有这些消息所用的总比特(bits)数,并且规定 receiver 猜得越准,loss 就越小。
从感性上来理解,生成模型的采样过程实际上也是在猜,猜得越准,采样结果越真实,代表其建模的分布越接近于真实的数据分布。
最优比特传输问题实际上是一场数据压缩游戏。以往有工作已经证明,在使用 arithmetic coding(算术编码) 和 bits-back coding 对消息进行编码(压缩)后传输的情况下,两者的压缩目标分别与 autoregressive models & diffusion models 的训练目标相对应。也就是说,数据压缩与训练两种模型的 loss 函数(autoregressive 是负对数似然;diffusion 是 KL 散度)之间存在着等价关系。
autoregressive models 是语言生成领域的 SOTA,但在图像生成这边却没那么能打。与离散形式的语言不同,图像是连续形式的数据,并且像素之间不存在天然的顺序关系——对于图像中的像素,似乎没有什么理由要求一定要先生成某个像素后再生成另一个,而一句话中的各个词之间的顺序却是有严格意义的。更尴尬的是,如果按 autoregressive 的玩法,图像中有多少个像素,那么就需要对应数量的步骤去生成。
反观 diffusion models,它们在图像生成领域大红大紫,以一种更自然地方式来生成图像——这是一种去噪的过程,从一张纯噪声图开始,通过不断减少噪声来达到 "coarse-to-fine" 的效果。但是,对于离散形式的数据,扩散(加噪)过程中的噪声也相应是离散的,而模型在去噪过程中估计的噪声天然是连续形式的,于是影响了去噪效果,导致其通常打不过 autoregressive models。作者认为这很可惜,毕竟 diffusion models “解耦”了变量(比如像素)数与生成步数,也就是不需要像 autoregressive models 那样逐个变量生成。
但是,作者是个执着 boy —— 他坚信连续形式的生成才是王道,就算对于离散形式的数据也一样!基于此信念,BFN 开启了它的一生~

玩出个性:BFN 的游戏方式
玩游戏的人都知道,虽然游戏体制一样,但各人都会以自己的方式玩出个性,现在就让我们一起来看看 BFN 是如何在这场数据压缩游戏中玩出个性的。

为了便于讲故事,作者给 sender & receiver 分别起了名字:Alice & Bob。在游戏开始前,Bob 会对数据分布进行 yy —— 设置一个先验(prior),并假设数据服从这种分布(各维度上的变量独立同分布),作者将其命名为"input distribution"(输入分布)。对于连续型数据,prior 设为 标准高斯分布(standard normal distribution);而对于离散型数据,prior 则设为各类别概率均等的 类别分布(categorical distribution)。
在每轮信息的传输过程中,由于势单力薄,因此 Bob 会抱神经网络的大腿——将输入分布的参数喂给 BFN,后者会输出另一个被称作 "output distribution"(输出分布) 的参数,输出分布也是对原始数据所服从的分布进行建模。
然后轮到 Alice 出场,她通过对原始数据加噪来构建一个 "sender distribution"(发送者分布) 并从中采样,采样结果就作为消息发送给 Bob,这些消息就是 Bob 的观测样本。
接着,Bob 也照着 Alice 的套路玩起了加噪,并使用同样的噪声分布。他先从输出分布中采样出样本,然后再对样本加噪。由于以单个输出样本猜中 Alice 手上的原始数据的可能性较低,因此 Bob 采取了暴力大法 —— 他采样了输出分布的所有可能的结果(相当于穷尽了分布中所有类别的样本),并且对它们加噪后的结果加权求和,以此作为对观测样本的猜测结果,其中每个样本的权重就是它们的采样概率。由此可见,这个猜测结果是(Bob 构造的)噪声样本在输出分布上的期望。
Bob 在以上过程中也相应构造了一个分布,被称作 "receiver distribution"(接收者分布),它建模的是观测样本(噪声数据)所服从的分布。
通过以上可知,发送者分布是观测样本真实服从的分布,而接收者分布是 Bob 在观测到样本前自己猜测的观测样本可能会服从的分布。
最后,Bob 会根据收到的消息并利用贝叶斯推断的方法(即:通过观测变量计算出后验来更新先验)来更新输入分布。 更新完毕后,随即开启下一轮游戏。
理想情况下,经历许多轮游戏后,Bob 就会猜得越来越准,从而最终 Alice 直接将原始(不带噪声的)数据传过去,Bob 也能猜中,简直准过算命先生!
既然是游戏,就会有 cost,玩家的目标就是尽力让 cost 变低甚至为0,而这场游戏的 cost(其角色等价于 loss function) 则规定为发送者分布与接收者分布的 KL 散度,这个值越小,Alice 传输消息所用的比特数就会越少。根据 CW 在上一节中提到的,在一定条件下,这种以 KL 散度为 loss function 的玩法与数据压缩存在着等价关系。
于是,Bob 猜得越准,则接收者分布对发送者分布就拟合得越好,从而 Alice 传输消息所用的比特数就越少,代表数据压缩率越高。
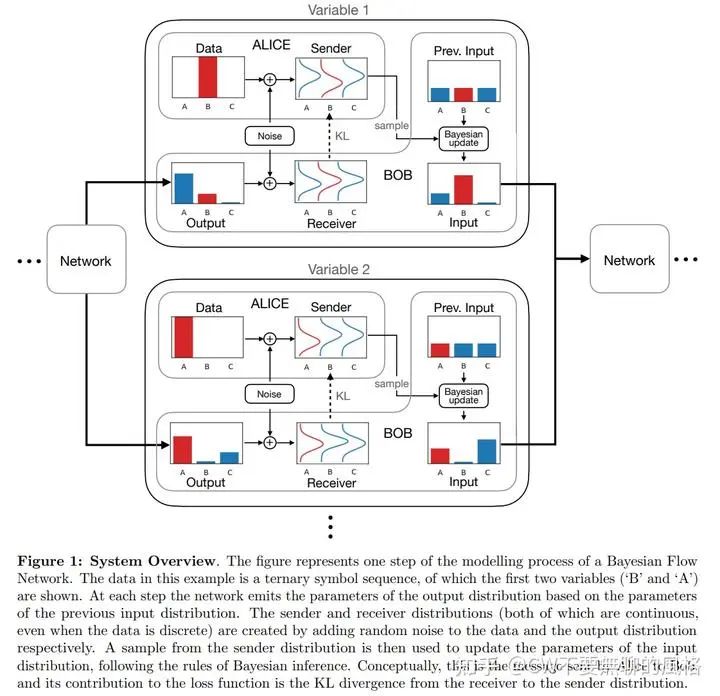
另外,有一个与输入分布和输出分布(两者均是对原始数据的分布建模)相关的关键点:输入分布是不包含上下文信息的,因为它首先假设数据中所有维度上的变量都是独立同分布的,并且后续又是通过贝叶斯更新(同样在各维度上独立进行)来接收信息;而输出分布由 BFN 构造,它以输入分布的参数作为输入,将各维度上对应的参数综合起来,进行了联合处理,使它们发生交互,于是输出分布包含了上下文信息。
比如对于一幅图像中的所有像素,在它们共同组成该图像前,都拥有各自独立的个性,这种个性就由贝叶斯大法来负责研究;而它们“聚在一起”组成这幅图像时,就需要“相互协调分工”(像素 A 负责当前景,像素 B 负责做背景),于是它们之间就存在一些协作关系,相互关系通常比较复杂(玄),这种关系就通过深度学习(BFN)来捕(炼)捉(丹)。
可以认为,输入分布是数据在“自然条件”下所服从的分布,而输出分布是数据在一定条件下的条件分布。
由此我们也可以直观地感受到,BFN 结合了贝叶斯推断和深度学习的优势:前者提供了一种在数学上最优且精细可控的方式来收集和归纳关于数据中各变量的独立信息;而后者则擅长于整合变量之间的相互关系和找出它们之间的交互规律。
在这场游戏中,Alice & Bob 每玩一轮,BFN 就会“进化”一次,整个过程就相当于它的训练过程。假设 Alice & Bob 一辈子都玩这个游戏,游戏轮数 nn 取极限到 \infty\infty ,则定义在离散时间步上的 nn 步 loss 函数就可以演变为连续时间上的形式,这时贝叶斯更新过程也相应变为贝叶斯信息流(bayesian flow),它由数据不断地将有效信息馈入神经网络中,最终造就出性能优秀的 BFN。
作者说,相比定义在离散时间上的形式,定义在连续时间上的 loss 函数在数学上会更简单、更容易计算,并且在训练完成后,BFN 可以在任意步数的离散时间步上进行推理和采样生成。 在正常情况下,生成质量会随着步数的增加而提高,相当于 "coarse-to-fine" 的效果。
主角光环:BFN 的天然优势
每部作品的主角都少不了主角光环,在这一章 CW 就浅浅地炫一下 BFN 的“圣光”。

由于 BFN 的输入是数据分布的参数,因此,尽管最终要生成的目标数据是离散的,在生成过程中其输入输出也是完全连续且可微的。 比如,对于离散的多类别数据,其服从类别分布,但该分布的参数依然是连续的实值。
纵观前文提及的几种生成模型,BFN 与 diffusion models 最为相似,但后者在应对离散数据时,要么是在离散的数据空间与连续的 embedding 空间之间做映射,要么就是将连续扩散的过程约束到 probability simplex 中,诸多限制,勉强则没有幸福~
而 “连续性”(continuity) 可谓是 BFN 內在的固有屬性, 这得益于它的输入是概率分布的参数,能够很自然地应对离散形式的数据,也就无需对现有的系统做约束。比如还是对于离散的多类别数据,BFN 的输入是类别分布的参数,是连续的实值(输出也是),但最终采样出来的结果却能够自然地处于 probability simplex 中。
在应对离散数据时,BFN 的这种天然基因还减少了参数的设计空间(无需设计离散数据空间与连续 embedding 空间之间的映射函数),能够直接对数据的负对数似然进行优化,而以往基于 diffusion models 的方法通常需要设计简化的 loss 函数或添加辅助 loss 项以稳定训练。
哦,还有,如前文所说,这种天然的“连续性”基因为基于梯度指导的采样生成和少步生成提供了可能。
比起 diffusion models,BFN 的输入相对来说没那么 noisy,因为后者的生成过程是从一个先验分布开始的(若提前了解到数据的分布,那会更有效果);而前者是从纯噪声开始的,没有(也无法)考虑真实数据的分布。作者认为,less noisy inputs 能够使 BFN 在大数据集上有更高效的拟合效果(收敛得更快)。
另外,BFN 无需像 diffusion models 那样设计一个前向(扩散)过程并且通过逆转它来实现生成,从而能够更方便地适配到不同类型的分布与数据。
总的来说,BFN 的天然优势可归纳为以下几点:
-
输入是连续可微的,能自然地应对离散数据; -
灵活地适配各种类型的数据与分布; -
为基于梯度指导的采样过程和少步生成提供了可能; -
能够直接优化似然函数,可以对数据的概率密度/值进行估计; -
less noisy inputs 使其在大数据集上收敛更快(暂未有实验支撑,纯属作者脑洞)。
内功心法:BFN 的数学框架
深度学习虽说是玄学,但它还是有其靠谱的道理——数学,这也可谓是其内功心法。

本章节会列出与 BFN 使用到的分布和函数相关的数学公式和性质,以及 loss 函数的推导,loss 包括离散时间和连续时间两种形式。
哦,请大家谨记,不要轻易让 BFN 退出前面的数据压缩游戏,这样会更容易理解。
输入与输出分布
记 维数据 所服从的分布参数为 维向量 , 则输入分布定义为:
根据上式, 数据 在每个维度上的变量 仅由对应维度上的分布参数 决定, 的概率密度即所有维度上的变量的联合概率密度, 等于各维度变量的概率密度 的乘积, 说 明每个维度上的变量都是独立的; 同时, 在每个维度上的变量 代表的都是同一种分布。
以上符合了输入分布的设定——数据在每个维度上的变量不发生交互。
输出分布是由 BFN 以输入分布的参数 为输入而产生的,此外,由于 BFN 是“在一场回合制游戏中打工”(结合第三章的故事背景),因此其还加入了时间变量 作为输入,以区分 Alice 和 Bob 的每一轮信息传输,这会更好地帮助 Bob 调控输出分布——因为 Alice 在每轮传输的信息方差都不一样,所以 Bob 也要灵活地对应调整,这样才能猜得更准。
记 BFN 为 , 则其输出为 , 从而输出分布定义为:
从上式可以看到, 虽然每个 仅由对应维度的 决定, 但后者却由所有维度的 即 产生, 因此 在每个维度上的变量都与其它维度发生了交互, 所以说输出分布拥有“上下文能力", 这是输入分布所不具备的。
发送者和接收者分布
发送者分布就是在原始数据上加噪后所得到的分布,也就是观测样本所服从的真实分布。
但 Alice 的加噪方式有些非主流, 不是直接对每一轮信息传输的噪声方差进行设置, 而是在每一轮对应设立一个称为“精度(accuracy)"的参数 , 来表示加噪后的数据 与原始数据 的相关(接近)程度。可以将其视作噪声方差的倒数, 越大, 的噪声程度越低, 其所含的与 相关 的信息量就越多。
于是, 发送者分布定义为:
在发送者分布中,各维度上的变量也是相互独立而不发生交互的。在整个游戏过程中,输入分布仅接收发送者分布馈入的信息(通过贝叶斯更新过程),从而保证了前者在各维度上的变量也没有交互。
接收者分布是 Bob 在输出分布上加噪后的结果,以此作为对观测样本所服从的分布的估计,定义为:
这是输入分布在输出分布上的期望,由于 Bob 不知道原始数据 ,因此这么做合情合理。另外,Bob 还开了外挂——这里的精度 在每轮游戏中都会与 Alice 保持一致。
贝叶斯更新
贝叶斯更新指的是根据贝叶斯推断来计算后验概率,以更新(校正)先验参数的过程。 放到这场游戏中,就是 Bob 在收到 Alice 传来的消息 后利用该观测样本来更新输入分布的参数 。
在这里,不妨设立一个“贝叶斯更新函数”来表示这个更新过程:
然而, 是个随机变量, 以上函数仅仅基于一个噪声样本计算出对应的一个值, 代表更新过程的其中一种可能性(不同的 会得到不同的 , 它们的取值都有概率性), 更科学地应该是要计算出其服从的分布。
于是, 设立对应的“贝叶斯更新分布”, 它在噪声样本上进行边缘化 (marginalizing out ), 即考虑了所有噪声样本的可能性:
其中 表示以 为中心的多元狄拉克分布(Dirac delta distribution)。
对于连续型和离散型数据,贝叶斯更新分布均具有“精度可加性”:
为了便于理解,证明过程 CW 将放到后续文章中,介时结合 BFN 对于连续和离散型数据的具体实现来进行说明。
加噪设置
每一轮信息传输由时间变量 表示, 而精度在每轮是不同的, 于是可将其看作是时间变量的函数: , 这样还可以同时兼容离散和连续时间的情况:在离散时间步的情况下,假 设总步数为 , 当前步为 , 则令 ; 而在连续时间的情况下, 可 以直接从区间 中均匀采样。
这时,我们定义 "accuracy schedule" 如下:
它是精度从起始时刻到当前时刻的积分, 是 的单调递增函数。
于是, 精度的计算方式为:
也就是说, 无论是连续还是离散时间步的情况, 时间变量 都是位于 区间内连续的小数。 只不过在离散时间步下,我们只能取到 在离散点上对应的取值: , 相当于只能在连续曲线上抓取其中的一些点,而不能获得完整的曲线。
这里的 accuracy schedule 类似于 diffusion models 中对噪声方差进行设置,因为它控制着发送者和接收者分布的方差,也就是噪声程度。 另外,也类似于 diffusion models 的噪声方差设置,在实际应用时, 是根据某种策略人为设定,而非计算积分而来。
贝叶斯流分布
贝叶斯流分布是当前时刻的贝叶斯更新分布的边缘分布,它对 BFN 的输入参数 进行边缘化:
根据前面提到的精度可加性,贝叶斯更新分布对于 和 的边缘化分布可以仅由 和 决定。 都是人为设定的, 而数据 是明确知道的, 于是这可以很方便地推导出每个时刻的贝叶斯流分布, 有点类似于 diffusion models 的扩散(前向)过程一一可以从原始图像 推导出各时刻的噪声图像 。
Loss 函数
假设 Alice 在这场游戏中一共向 Bob 传输了 条消息(噪声数据): , 最后再将原始数据 传过去, 则 loss 函数包含两部分:一部分是传输 条消息的所需的奈特数(nats), 记为 ; 另一部分是最后传输原始数据所需的奈特数, 记为 。
在 bits-back coding 的编码方案下, 等于发送者分布与接收者分布的 KL 散度。
由于有 轮游戏, 且每轮对应的 是随机变量, 具有有概率性, 因此 应该是 的期望:
注意, 第 轮的接收者分布由 确定, 此时 Bob 还未收到 Alice 的消息(也正因如此他才用接收者分布进行猜测)。
同理, 在 arithmetic coding 的编码方案下, 等价于重构 , 即在最后时刻的参数 下的负对数似然 :
同样地, 由于 的随机概率性, 是在边缘分布 下的期望。由于传输 只发生在最后一步, 因此 。
综合起来, 最终的 loss 函数就是:
以 VAE 的角度理解 loss 函数
熟悉 VAE 的朋友们知道, 其 loss 函数也包含两部分:重构损失 以及 对于隐变量的后验分布与其先验分布的 KL 散度 , 其中 代表隐变量。
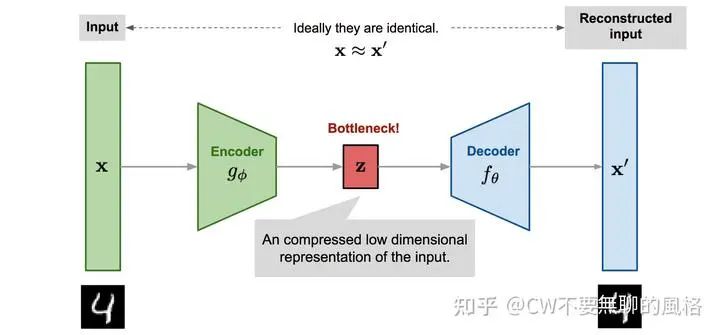
在这里,其实我们也能够以 VAE 的角度来理解 BFN 的 loss 函数。
不妨将 Alice 传输的消息: 看作是隐变量序列, 然后“照葫芦画漂”, 将隐变量的后验分布 等同于 BFN 的发送者分布:
在这里我们用 来表示其实更符合 变分法(Variational Method) 的形式(VAE 实际是根据变分法来玩的, 只不过其选取了后验分布 作为隐变量的简单分布 )。
既然先验是 , 那么相应地, 隐变量的先验分布就选取接收者分布:
然后, VAE 解码重构的概率分布就用输出分布来充当:
于是,重构损失就是对应的负对数似然:
最后,loss 函数就是发送者分布和接收者分布的 KL 散度加上在输出分布下的负对数似然:
离散时间步的 loss 形式
在离散时间步和连续时间的情况下, 的形式会有所不同; 而 由于只发生在最后一步, 因此没有影响。
根据 蒙特卡洛采样, 我们可以将 中的 步求和改写一下, 近似为:
其中 代表从 1 到 的整数均匀分布。
结合精度的可加性, 对于贝叶斯更新分布的那部分期望可以转换为用贝叶斯流分布来表示:
于是,最终得到:
这种形式的优势在于我们不需要计算 步求和, 而可以通过蒙特卡洛采样来近似计算。
连续时间的 loss 形式
现在来推导下 在连续时间情况下的形式。
当 , 我们给予以下定义:
于是,结合上一节在离散时间步情况下的推导结论,有:
其中 是定义在 区间的连续型均匀分布。
进一步,作者在 paper 中提出了对于发送者分布和接收者分布之间的 KL 散度的泛化形式:
其中 是将原始数据所在空间映射到 Alice 传输的消息(即观测样本)空间的函数; 是在 定义在观测样本空间上的具有有限期望和方差的单变量分布, * 代表两个概率分布的卷积操作, 代表正态分布, 为常数。
当 时, 对于具有有限期望 与方差 的连续型单变量概率分布 , 作者还进一步证明了有以下结论:
这样,就能够将发送者分布和接收者分布之间的 KL 散度转变为两个正态分布之间的 KL 散度,从而方便计算。
根据统计学中的卷积定义,两个相互独立的随机变量之和 所服从的分布 就是 它们这两个分布的卷积:
在这基础上, 如果我们能构造出 的形式,那么根据正态分布的性质, 就可以顺理成章地得到目标结论:
现在,有请大家和 CW 一起齐心协力来推导出该结论。
首先,构造一个随机变量序列: ,其中 是一个有限方差。接着, 为了便于后续的推导, 定义以下变量:
, ,
于是,根据前面所说的卷积定义以及正态分布的性质,就有:
所以, 只要我们能够证明当 时, ,那 么就可以成功地证明我们的目标。
现在,我们需要抱一下大腿一一根据 Lyapunov central limit theorem(李雅普诺夫中心极限定理):
若存在 , 使得 , 则
同时, 当 , 有: , 从而 。于是, 我们的目标转变为求证“李雅普诺夫条件":存在 。
为简单起见, 令 , 则 时, 是半正态分布的第三矩(the third moment of the half-normal distribution) 。假设 , 那么: 。
另外, 由于 都是有限值, 于是 肯定存在一个上限值, 不妨设其接近于常数 。
综合起来,我们可以得到:
这说明“李雅普诺夫条件”是可以成立的。于是,目标结论: 得证。
如今,我们就能够将发送者分布和接收者分布之间的 KL 散度转变为两个正态分布之间的 KL 散度(推导过程见附录):
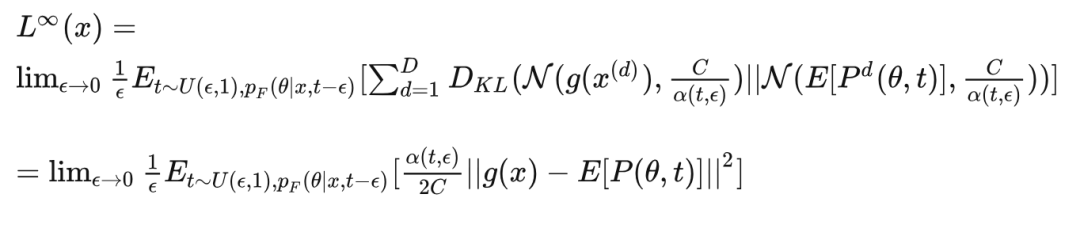
其中:
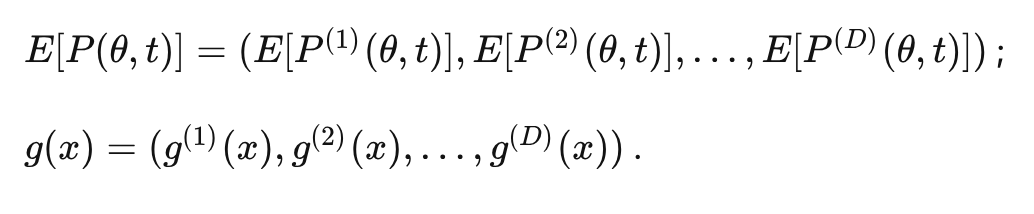
咦,不小心发现:
于是, 最终整理得到:
以上就是 在连续时间情况下的形式。
采样生成
借助于 BFN 的力量, 经过这场游戏后, Bob 已经能够利用接收者分布来较好地拟合发送者分布, 相当于 Bob 能够以较高的准确率猜对每条消息。于是, 给定任意先验 , 都可以多次迭代地利用 来就纠正(更新)它,待自认为有足够自信后,才拿最终的 来采样生成数据 。
具体地,整个流程如下:
给定先验 , 假定我们计划要将其更新 次后才拿来生成样本, 那么先设定好对应每一步的精度: , 对应每一步的时间变量为: 。
经过训练后, 由于接收者分布已经近乎完美拟合发送者分布, 因此在每一步, 就可以直接从接收者分布 中采样出观测样本 , 这相当于先从输出分布 中采样出 , 然后再从发送者分布 中采样出 。接着, 再利用贝叶斯更新: 完成对先验的校正。
待 次更新完毕, 最终就使用 从输出分布 中采样生成样本 。
OK,了解了以上过程,现在问题来了:
-
问: 为何不直接从发送者分布中采样观测样本?
那是因为在训练时(也就是 Alice 和 Bob 在玩游戏时)是有真实数据的啊!然而在推理时我们手头上却是空空如也~于是无奈之下,必须根据先验参数从输出分布中采样,以此作为对真实数据的估计;然后再以这个估计样本为条件从发送者分布中采样出观测样本。而根据定义,这个过程等价于根据先验参数直接从接收者分布采样:
-
问: 最后一步从输入分布 中采样作为结果可以吗?
可以,但使用输出分布会更好。
其中一个原因如前文所说:输出分布有上下文信息,生成结果会更加协调。
而另一个原因是:在训练过程中, (连续时间的情况下是 ) 不断拉近接收者分布和发送者分布,在每一步中,两者使用相同的噪声强度,前者在输出分布的采样结果上加噪,后者在原始数据上加噪,这就相当于隐式地在拉近输出分布与真实数据分布;相反,输入分布由始至终仅通过噪声样本馈入原始数据的信息,相当于其信息来源不那么透明与直接。因此,从这个角度看,输出分布会更加令人有好感~
-
问: 能否一步生成!?
这真的是一个非常犀利的问题!毕竟在如今 diffusion model 大肆虐杀的时代,若是能够实现高质量的一步生成,那么就能怼掉那嚣张的家伙了。
若要 BFN 实现一步生成, 一种方式是先通过多步迭代更新先验, 然后再保留下最后一步更新完的先验 , 以后都从 中采样生成。
然而, 我们不应该由始至终都用同一个 , 因为 本身也是随机变量! 它通过不同的观测样本获得不同的数据信息。如果你一直都用同一个 来生成最终的样本, 那么就相当于始终围绕着一个训练集中的原始样本, 这样生成的结果就会缺乏多样性。
另一种方式是直接根据预设的先验 来从输出分布中采样出最终结果。然而, 由于没有经过后验更新, 因此缺乏真实数据的信息, 从而以 为条件的输出分布就与真实的数据分布相差甚远~
虽说在训练过程中隐式地将输出分布与数据分布对齐, 但想要拟合得好, 也是有条件的一一输出分布在合适的输入分布参数 的条件下会拟合得更好, 当 所含的数据信息就越多(观测样本携带的数据信息越多)时, 输出分布就越接近数据分布。
(若你们还有问题,欢迎在评论区积极提出,CW 会把有意思的贴上来~)
附:两个多元正态分布之间的 KL 散度
对于多维变量 , 记 , 如今有请各位客官一同来推导 。
先将多元正态分布的概率密度公式代入,看看会发生什么:
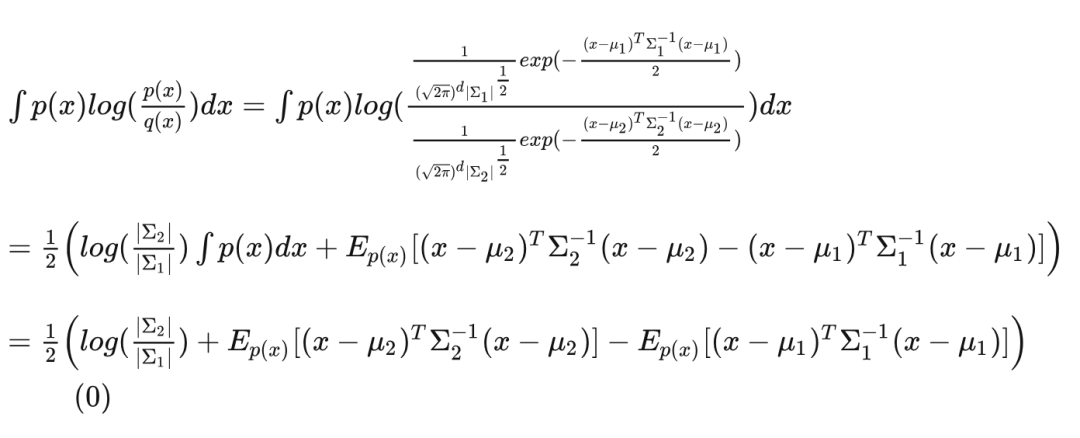
现在关键是要解决后两项, 不妨先从其中的 着手。在此我们需 要借助下 matrix trace(矩阵的迹)的性质:
-
, 其中 为矩阵; -
对于列向量 和矩阵 是标量, 于是: ; -
, 其中 为矩阵, 为标量.
由于 是标量, 因此借助于以上性质进一步玩下去:
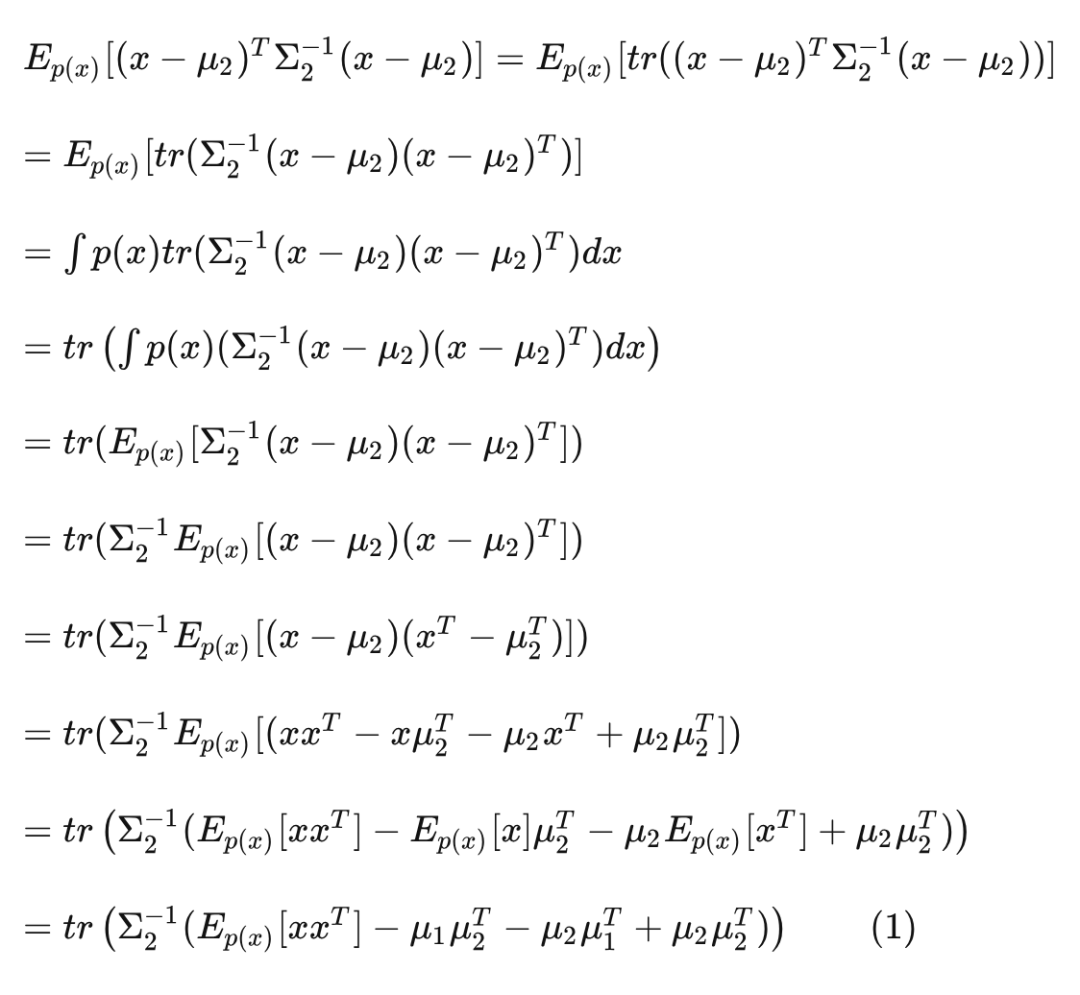
如果我们尝试将上式中的 替换为 ,就会发现:
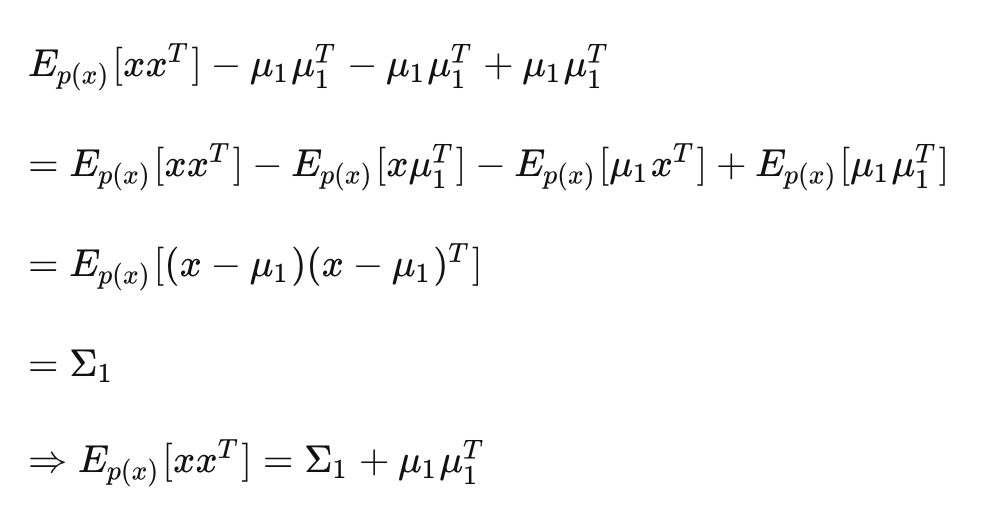
(其实就是这个性质:)
将其代入式 (1) ,得到:
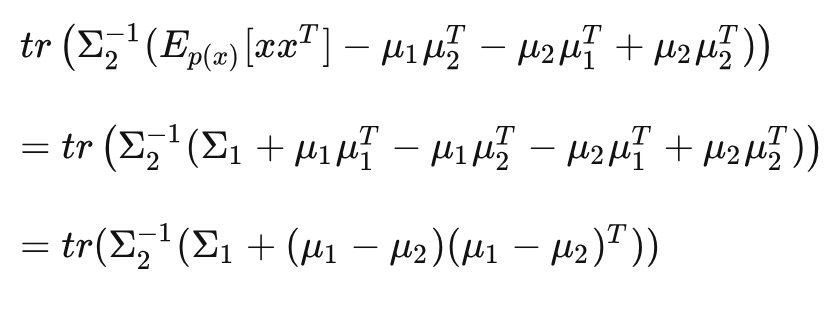
再次利用 matrix trace 的性质:
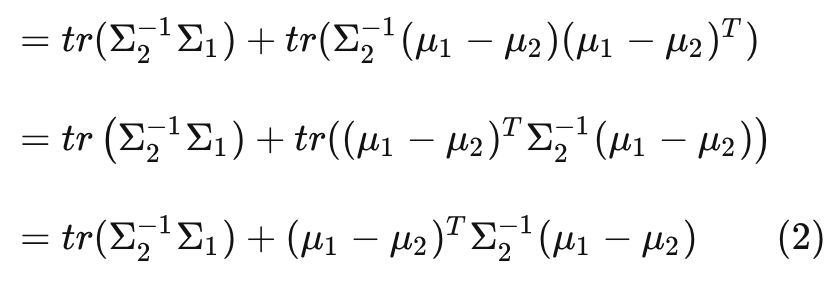
即:
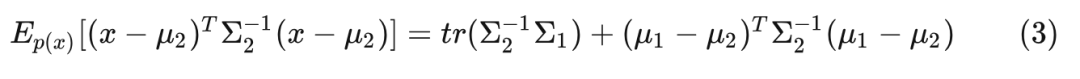
同理, 对以上 (2) 式进行替换: , 可得到:
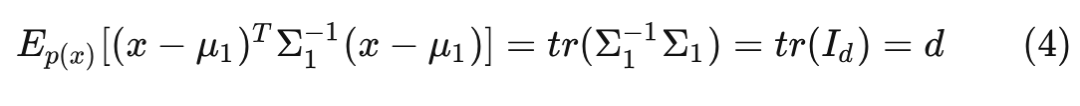
其中 为 维单位阵。
Now, 可以奏响片尾曲了! 将 式代入 (0) 式, 得到:
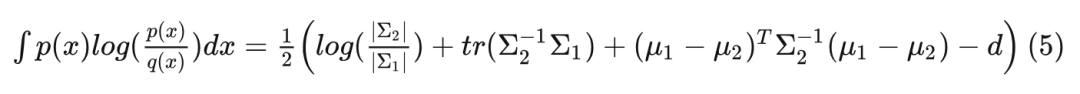
以上就是两个多元正态分布之间的 KL 散度的推导形式。
当两个分布的(协)方差相等时,即将 代入 (5) 式,就会看见:
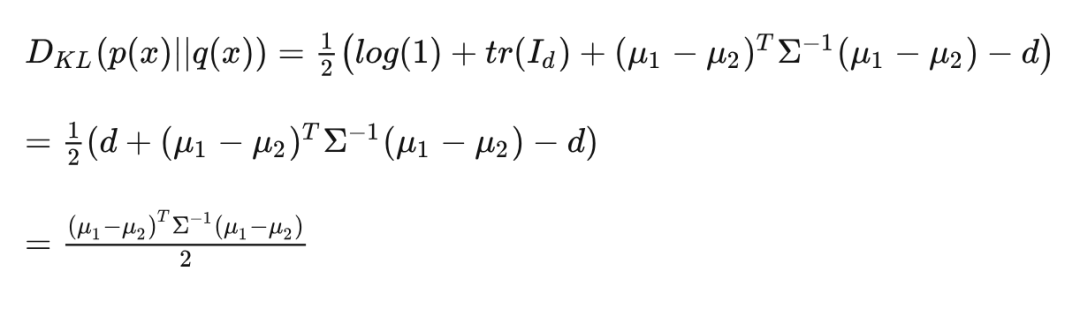
这就是 BFN 在连续时间情况下的 , 其中 。
To Be Continued
最后提一点,BFN 并非“无条件”地直接对数据分布建模,而是:在给定的先验(输入分布的参数) 下,整合各维度变量的相关信息(探索上下文信息),然后输出一个与输入分布相依赖的输出分布,它其实是在 的约束下尽可能地逼近真实数据分布。由于 携带着数据信息,因此好的 十分重要。
本文目标在于令大家对 BFN 的整体框架和运作流程有个基本认识与理解。在本系列的后续文章中,你将会看到 BFN 在面对不同类型的数据:连续(continuous)数据、离散化(discretised)数据 以及 离散(discrete)数据 时的具体实现。
CW 估计心急的朋友们已经迫不及待想知道 BFN 在面对具体任务时是如何 work 的,但还请大家稍安忽躁,可以喝多几杯手冲咖啡,好好地回味下本文的内容(时刻不忘履行“咖啡传教士”的职责,hh)~


公众号后台回复“1024”参与1024活动抽奖~
极市干货
点击阅读原文进入CV社区
收获更多技术干货
