前言
前几天和阿里的朋友聊天,得知大厂里经常考算法,还要考算法等级,分高级、中级、初级三个大等级,每个阶段的程序员需要考对应等级的算法,在大厂确实不易。
但是,算法算是研发人员的需要掌握的基础底层知识,所以想成为一名优秀的程序员还是有必要掌握的一些算法的,下面我们就一起来学习一下“堆排序”。
一、堆是什么?
堆是一种特殊的完全二叉树。
1.1、二叉树
定义:二叉树是每个节点最多有两个子节点的树结构。
特点:
每个节点最多有两个子节点,即二叉树不存在大于2的节点;
二叉树的子树有左右之分,其子树的次序不能颠倒;
1.2、满二叉树
定义:除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉,一颗深度为k且有2^k-1个节点的树成为满二叉树
例如下图深度k=3,节点数N=7=2^3-1
特点:
每层都是满的
叶子节点(度为0的节点)全部在最底层
1.3、完全二叉树
定义:
深度为k的具有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中编号为1~N的节点一一对应时,称之为完全二叉树
特点:
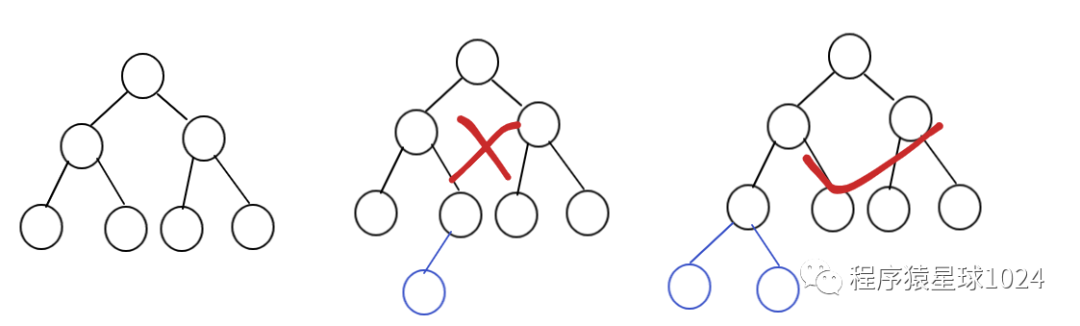
1.4、堆的特点:
父节点的值 大于等于或小于等于 子节点的值,根据大于和小于也分成了二种
完全二叉树
父节点的值 大于等于 子节点的值的为大顶堆。
父节点的值 小于等于 子节点的值的为小顶堆。
举例:
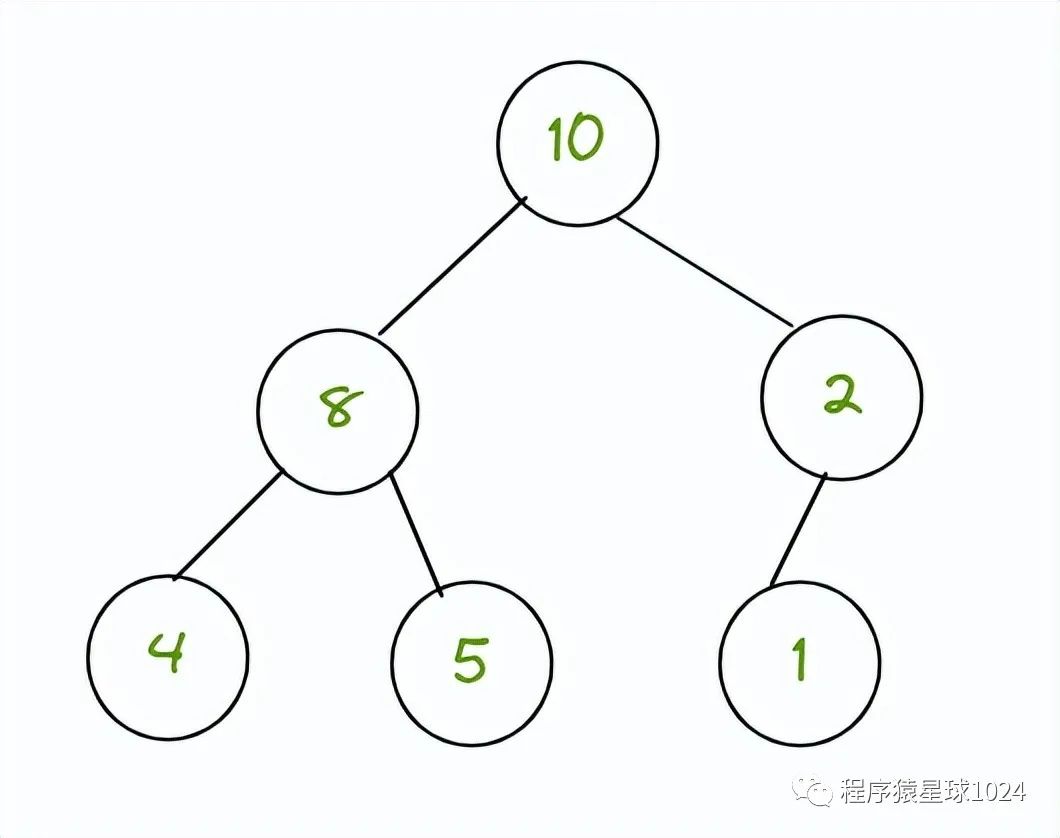
二、如何通过堆来排序?
给定一个待排序的数组tree = [a1,a2,a3,...an] 进行如下操作:
1. 建堆:将数组 tree 建成一个堆
2. 输出:删除根节点,将其输出,然后将最后一个叶子节点移动到根节点
3. 调整:移动之后的树不满足堆的性质,此时需要进行一轮调整,使其成为一个新堆
4. 不断进行步骤2、3 得到的输出序列就是排好的序列
三、如何构建堆?

根据建堆操作的不同,可分为筛选法建堆的堆排序和插入法建堆的堆排序
3.1、 筛选法
(1) 将数组按顺序生成一个完全二叉树。
(2) 按照从下到上,从右到左的原则扫描父节点,对每一个父节点比较其左右子节点,若子节点大于父节点,则交换父子节点,并向下继续检查有没有破坏堆结构。
(3) 反复执行步骤(2)直至根节点。

//建立大顶堆function buildMaxHeap(tree, n) { //从最后一个节点开始 let last_node = n - 1
//当前节点的父节点 let parent = (last_node - 1) / 2 for (let i = parent; i >= 0; i--) {
heapify(tree, n, i)
}
}/**
*
* @param {*} tree 所有节点数组
* @param {*} n 数组长度
* @param {*} i 当前需heapify处理的节点
* @returns */function heapify(tree, n, i) {
if (i >= n) {
return }
let c1 = 2 * i + 1,//左节点 c2 = 2 * i + 2//右节点 let max = i //最大值 if (c1 < n && tree[c1] > tree[max]) {
max = c1
}
if (c2 < n && tree[c2] > tree[max]) {
max = c2
}
if (max != i) {
swap(tree, max, i)
heapify(tree, n, max)
}
}//交换节点function swap(arr, i, j) {
let temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}let tree = [2, 5, 3, 1, 10, 4]let n = tree.lengthconsole.log('创建堆前结果', tree);// [ 2, 5, 3, 1, 10, 4 ]buildMaxHeap(tree, n)console.log('创建堆结果', tree);//[ 10, 5, 4, 1, 2,3.2、 插入法
(1) 生成一颗空的完全二叉树,并将第一个数据元素作为根节点,
(2) i从第二个数据元素开始,将第i个数据元素插入二叉排序数的第i个位置
(3) 将被插入的元素与其父节点进行比较,若大于父节点,则与父节点交换,交换后继续向上检查,直到根节点
(4) 反复执行(2)(3)直到所有元素插入到完全二叉树中并调整完成,得到一个大顶堆

//创建大顶堆function buildMaxHeap(tree, n) { for (var i = 0; i < n - 1; i++) { for (var j = i + 1; j > 0; j--) { let parent = Math.floor((j - 1) / 2); if (tree[j] > tree[parent]) { swap(tree, j, parent); } } }}//交换节点function swap(arr, i, j) { let temp = arr[i]; arr[i] = arr[j]; arr[j] = temp;}let tree = [2, 5, 3, 1, 10, 4];let n = tree.length;console.log("创建堆前结果", tree); //[ 2, 5, 3, 1, 10, 4 ]buildMaxHeap(tree, n);console.log("创建堆后结果", tree);//[ 10, 5, 4, 1, 2, 3 ]四、堆排序
删除根节点,将其输出,然后将最后一个叶子节点移动到根节点
移动之后的树不满足堆的性质,此时需要进行一轮调整,使其成为一个新堆
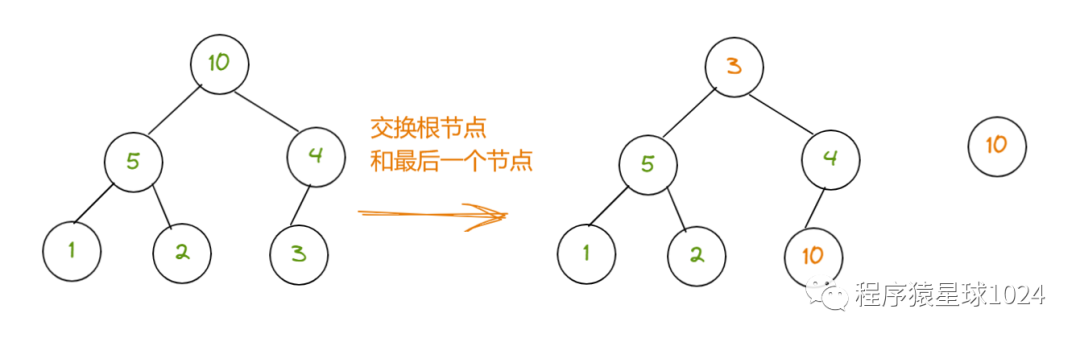
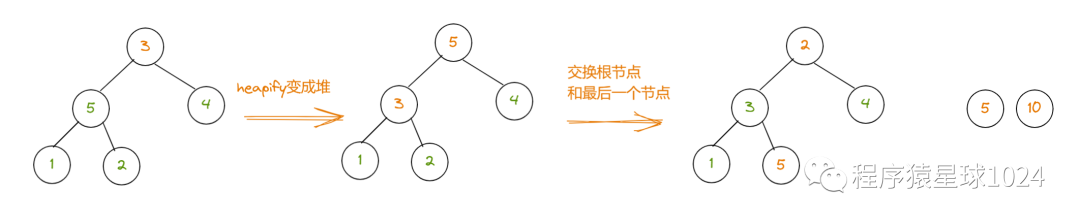



//筛选建立大顶堆function buildMaxHeap(tree, n) {
let last_node = n - 1;
let parent = (last_node - 1) / 2;
for (let i = parent; i >= 0; i--) {
heapify(tree, n, i);
}
}//插入创建大顶堆function buildMaxHeap2(tree, n) {
for (var i = 0; i < n - 1; i++) {
for (var j = i + 1; j > 0; j--) {
let parent = Math.floor((j - 1) / 2);
if (tree[j] > tree[parent]) {
swap(tree, j, parent);
}
}
}
}/**
* 堆调整
* 找出左右子节点最大值,并与父节点交换
* @param {*} tree 所有节点数组
* @param {*} n 数组长度
* @param {*} i 当前需heapify处理的节点
* @returns */function heapify(tree, n, i) {
if (i >= n) {
return;
}
let c1 = 2 * i + 1, //左节点 c2 = 2 * i + 2; //右节点 let max = i; //最大值 if (c1 < n && tree[c1] > tree[max]) {
max = c1;
}
if (c2 < n && tree[c2] > tree[max]) {
max = c2;
}
if (max != i) {
swap(tree, max, i);
heapify(tree, n, max);
}
}//交换节点function swap(arr, i, j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}//筛选堆排序function heap_sort(tree, n) {
buildMaxHeap(tree, n, 0);
console.log("创建堆后结果", tree);//[ 10, 5, 4, 1, 2, 3 ] for (let i = n - 1; i >= 0; i--) {
//交换根节点和最后一个节点 swap(tree, i, 0); //砍断最后一个节点,即最后一个节点是最大值 heapify(tree, i, 0);
}
}//插入堆排序function heap_sort2(tree, n) {
buildMaxHeap2(tree, n, 0);
console.log("创建堆后结果2", tree);//[ 10, 5, 4, 1, 2, 3 ] for (let i = n - 1; i >= 0; i--) {
//交换根节点和最后一个节点 swap(tree, i, 0); //砍断最后一个节点,即最后一个节点是最大值 buildMaxHeap2(tree, i, 0);
}
}let tree = [2, 5, 3, 1, 10, 4];let n = tree.length;console.log("创建堆前结果", tree); //[ 2, 5, 3, 1, 10, 4 ]heap_sort(tree, n);console.log("堆排序后结果", tree); //[ 1, 2, 3, 4, 5, 10 ]console.log('=========================');let tree2 = [2, 5, 3, 1, 10, 4];let n2 = tree.length;console.log("创建堆前结果2", tree2); //[ 2, 5, 3, 1, 10, 4 ]heap_sort2(tree2, n2);console.log("堆排序后结果2", tree2); //[ 1, 2, 3, 4, 5, 10 ]五、时间复杂度分析
5.1、 筛选法
(1) 将数组按顺序生成一个完全二叉树。
(2) 按照从下到上,从右到左的原则扫描父节点,对每一个父节点比较其左右子节点,若子节点大于父节点,则交换父子节点,并向下继续检查有没有破坏堆结构。
(3) 反复执行步骤(2)直至根节点。
建堆最好时间复杂度 O(n):
当按顺序生成的完全二叉树就满足堆的要求的时候,那么步骤(2) 中每个节点只需要进行两次比较:
(1)左右孩子比较
(2)与最大的孩子节点进行比较
建堆最坏时间复杂度O(n):
当每次检查都需要交换并且一直检查到叶子节点时:第 k层节点最多需要向下移动 h-k次,h为堆高。
由二叉树的性质可知,第 k层最多有 2^(k-1)个节点

5.2、 插入法
(1) 生成一颗空的完全二叉树,并将第一个数据元素作为根节点,
(2) i从第二个数据元素开始,将第i个数据元素插入二叉排序数的第i个位置
(3) 将被插入的元素与其父节点进行比较,若大于父节点,则与父节点叫喊,交换后继续向上检查,直到根节点
(4) 反复执行(2)(3)直到所有元素插入到完全二叉树中并调整完成,得到一个大顶堆
建堆最好时间复杂度 O(n):
每次插入只需要比较一次,故最好时间复杂度为 O(n)
建堆最坏时间复杂度 :

每次插入后都发生交换,并一直检查到根节点;第 k层节点最多需要向上移动 k-1 次,由二叉树的性质可知,第k层最多有
2的(k-1)次个节点, h为堆高

5.3、堆排序时间复杂度

六、空间复杂度
使用自身存储,所以是O(1)
七、总结
以下均为个人总结,如有问题欢迎指点:
堆排序的步骤:建堆 -> 首尾交换,断尾重构 -> 重复第二步,直到断掉所有尾巴
稳定性:堆排序存在大量的筛选和交换过程,可能造成不相邻的两个等值节点之间的顺序会发生层级变化,最终导致这两个等值节点在序列中的相对位置发生变化。属于不稳定的排序算法。
使用场景:堆排序在建立堆和调整堆的过程中会产生比较大的开销,在元素少的时候并不适用。但是,在元素比较多的情况下,还是不错的一个选择。尤其是在解决诸如TOP-K一类问题时,几乎是首选算法。





