线性回归

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。

最小二乘法

最小二乘法是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配。最早接触最小二乘法，应该是在高中初等数学中。要想拟合直线达到最好的效果，就是将直线和所有点都近，即与所有点的距离之和最小。

比如样本点与直线之间的“距离”，代入方程计算出距离等于，如图所示。

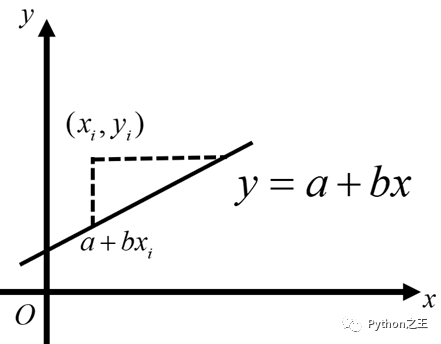
很显然，这个值越小，则样本点与直线间的距离越小。最小二乘法的距离不能用点到直线的距离来表示样本点与直线之间的距离。

如果有个点：，使用下面的表达式来计算这些点与直线的接近程度。

使得上式达到最小值，对进行求导：

对进行求导：

上面两个等式构成方程组，求解和，得到斜率计算公式如下。

由

得到。

因此，得到，这个直线方程称为线性回归方程，和是线性回归方程的系数（回归系数）。

在某化工生产过程中，为研究温度（单位：摄氏度）对收率（单位：%）的影响，测得一组数据如表所示，试根据这些数据建立以与之间的回归方程，并预测时，的值。

x	100	110	120	130	140	150	160	170	180	190
y	45	51	54	61	66	70	74	78	85	89

这是一道关于最小二乘法高中应用题，代入公式，，，。

因此， x与 y的回归方程为：。当，代入回归方程，计算出。

在机器学习中，最小二乘法常用矩阵法进行介绍和使用。假设函数的矩阵表达方式为：。

其中，函数为的向量，是的向量。其中代表样本的个数，代表样本的特征数。

损失函数定义为。

其中是样本的输出向量，维度为，这里的主要为了求导后系数为1而设置的。

根据最小二乘法的原理，对损失函数对向量进行求导。

得到，整理后得到。

最小二乘法需要计算的逆矩阵，但是有可能它的逆矩阵不存在，这样就没有办法直接用最小二乘法了，这是需要使用梯度下降法，可以通过对样本数据进行整理，去掉冗余特征，让的行列式不为0，然后继续使用最小二乘法。

梯度下降法

在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，这里就对梯度下降法做一个完整的总结。

先从一个生活实例下山说起。想象一下你出去旅游爬山，爬到山顶后已经傍晚了，很快太阳就会落山，所以你必须想办法尽快下山，然后去吃海鲜大餐。问题就来了，怎么下山比较快？这时，你会马上选择从最陡的方向下山，这就是梯度下降法的现实例子，下面来正式学习下梯度下降法的基本思想。

在微积分里面，对二元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。比如函数分别对求偏导数，求得的梯度向量就是，简称。

点的具体梯度向量为，如果是三元函数的参数，就是，依此类推。

函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度，然后朝着梯度相反的方向，就能让函数值下降的最快！

因为梯度的方向就是函数之变化最快的方向。利用这个方法，不断地反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程，求取梯度就确定了最陡峭的方向

在一座大山上的某处位置，由于不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得已经到了山脚。

当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

假设函数表示为 , 其中为模型参数，为每个样本的个特征值。增加一个特征，这样函数就表示为，损失函数采用定义为，其中表示第个样本特征，表示第个样本对应的输出，为假设函数。

确定当前位置的损失函数的梯度，对于进行求导，得到其梯度表达式。用步长乘损失函数的梯度，得到当前位置下降的距离。

这里的，在机器学习称为Learning rate，也是常说的学习率。如果太小，每次更新的步长很小，导致要很多步才能到达最优点，相反如果太大，每次更新步长很大，在快接近最优点时，容易因为步长过大错过最优点，最终导致算法无法收敛，甚至发散。

随着越来越靠近最低点，在该点处的斜率越来越小，即梯度值越来越小，但是因为，所以两者相乘后也越来越小，进一步导致值减小的越来越慢。

假设有一个单变量的函数，对其求导得到梯度，初始化起点，学习率。根据梯度下降的计算公式：，不断地迭代计算。

第1次迭代，。第2次迭代，。第3次迭代，。第4次迭代，。

经过4次迭代，已经基本靠近函数的最小值点0。

下面采用Python代码实现一个简单地梯度下降算法。场景是一个简单的线性回归的例子，具体代码如下。

# -*- coding: utf-8 -*-
# @Author: By Runsen

def func_1d(x):
    """
    目标函数
    :param x: 自变量
    :return: 因变量
    """
    return (x-1) ** 3 + 4


def grad_1d(x):
    """
    目标函数的梯度
    :param x: 自变量，标量
    :return: 因变量，标量
    """
    return  3*(x-1)


def gradient_descent_1d(grad, cur_x, learning_rate,precision,max_iters):
    """
    一维问题的梯度下降法
    :param grad: 目标函数的梯度
    :param cur_x: 当前 x 值，通过参数可以提供初始值
    :param learning_rate: 学习率，也相当于设置的步长
    :param precision: 设置收敛精度
    :param max_iters: 最大迭代次数
    :return: 局部最小值 x
    """
    for i in range(max_iters):
        grad_cur = grad(cur_x)
        if abs(grad_cur) < precision:
            break  # 当梯度趋近为0 时，视为收敛
        cur_x = cur_x - grad_cur * learning_rate
        print("第", i, "次迭代：x 值为 ", cur_x)

    print("局部最小值 x =", cur_x)
    print("局部最小值 y =",func_1d(cur_x))
    return cur_x

if __name__ == '__main__':
    gradient_descent_1d(grad_1d, cur_x=10, learning_rate=0.2, precision=0.000001, max_iters=10000)

####输出如下####
第 0 次迭代：x 值为  4.6
第 1 次迭代：x 值为  2.44
第 2 次迭代：x 值为  1.5759999999999998
第 3 次迭代：x 值为  1.2304
第 4 次迭代：x 值为  1.09216
第 5 次迭代：x 值为  1.036864
第 6 次迭代：x 值为  1.0147456
第 7 次迭代：x 值为  1.00589824
第 8 次迭代：x 值为  1.002359296
第 9 次迭代：x 值为  1.0009437184
第 10 次迭代：x 值为  1.00037748736
第 11 次迭代：x 值为  1.000150994944
第 12 次迭代：x 值为  1.0000603979776
第 13 次迭代：x 值为  1.00002415919104
第 14 次迭代：x 值为  1.000009663676416
第 15 次迭代：x 值为  1.0000038654705663
第 16 次迭代：x 值为  1.0000015461882266
第 17 次迭代：x 值为  1.0000006184752905
第 18 次迭代：x 值为  1.0000002473901162
局部最小值 x = 1.0000002473901162
局部最小值 y = 4.0

代码中选用了作为梯度下降的函数，经过18次迭代得到局部最小值，局部最小值。

线性回归实现

线性回归是处理一个或者多个自变量和因变量之间的关系，然后进行建模的一种回归分析方法。如果只有一个自变量的情况称为一元线性回归，如果有两个或两个以上的自变量，就称为多元回归。在sklearn中linear_model 模块几乎集成了所有线性模型，采用linear_model 中的可以实现linearRegression线性回归。

下面通过numpy随机生成散点，采用linearRegression进行回归，具体代码如下。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.linspace(0,30,50)
y = x+ 2*np.random.rand(50) 
plt.figure(figsize=(10,8))
plt.scatter(x,y)

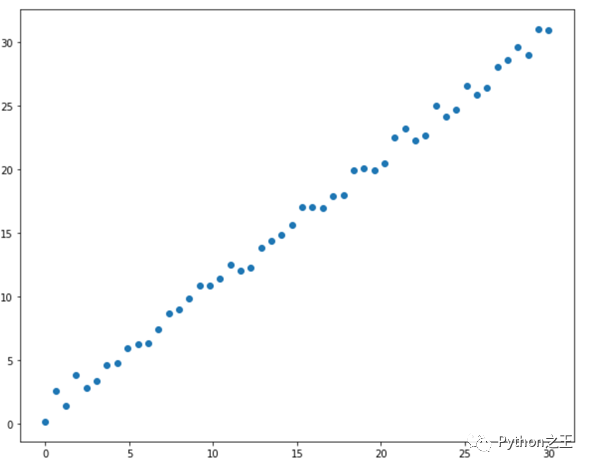
下面导入线性回归，训练数据，具体代码如下。

# 导入线性回归
from sklearn.linear_model import LinearRegression
# 初始化模型
model = LinearRegression()  
# 将行变列，得到x坐标
x1 = x.reshape(-1,1)   
# 将行变列  得到y坐标
y1 = y.reshape(-1,1)  
# 训练数据
model.fit(x1,y1) 
# 预测下x=40 ，y的值
print(model.predict(np.array(40).reshape(-1,1)))

####输出如下####
array([[40.90816511]]) # x=40的预测值

plt.figure(figsize=(12,8))
plt.scatter(x,y)
x_test = np.linspace(0,40).reshape(-1,1)
plt.plot(x_test,model.predict(x_test))

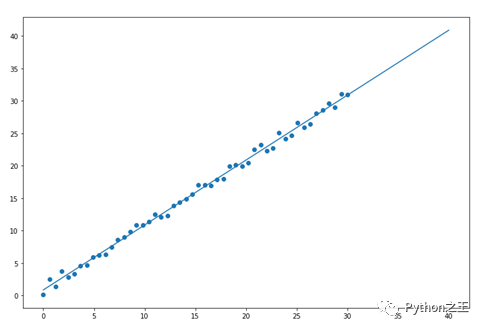可以通过打印model.coef_和model.coef_查斜率和截距，具体代码如下。

# 斜率
print(model.coef_)   
# 截距 
print(model.intercept_) 
####输出如下####

array([[1.00116024]])  
array([0.86175551])

从结果输出，得到线性回归方程：。在评价线性回归模型的性能，通常采用计算点到直线的距离的平方和，也是常说的均方误差（Mean Squared Error，MSE）。下面通过numpy计算MSE，具体代码如下。

print(np.sum(np.square(model.predict(x1) - y1)))

####输出如下####
16.63930773735106

除了sklearn实现线性回归，在Python中还有大量的第三方库实现线性回归，比如最常见的Numpy和scipy科学计算库。

import numpy as np
x = np.linspace(0,30,50)
y = x+ 1 + np.random.normal(0,0.1, 50)
# 一次多项式拟合，相当于线性拟合
z1 = np.polyfit(x,y,1) 
print(z1) 
p1 = np.poly1d(z1) 
print(p1) 

####输出如下####
[0.99912291 0.99942041]
0.9991 x + 0.9994

from scipy import stats
x = np.random.random(20)
y = 5*x +10+  np.random.random(20)
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
print("slope: %f    intercept: %f" % (slope, intercept))
print("R-squared: %f" % r_value**2)

####输出如下####
slope: 5.304534    intercept: 10.338254
R-squared: 0.977617

还有统计模块比较出名的Statsmodels中的OLS最小二乘法也可以实现线性回归，虽然Statsmodels在简便性上是远远不及SPSS和 Stata等数据分析软件的，但它的优点在于可以与 Python 的NumPy、Pandas有效结合。

import statsmodels.api as sm
import numpy as np
x = np.linspace(0,10,100)
y = 3*x + np.random.randn()+ 10
X = sm.add_constant(x)
mod = sm.OLS(y,X)
result = mod.fit()
print(result.params)
print(result.summary())

####输出如下####
[9.65615842 3.        ]
  OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       1.000
Model:                            OLS   Adj. R-squared:                  1.000
Method:                 Least Squares   F-statistic:                 7.546e+31
Date:                Tue, 14 Apr 2020   Prob (F-statistic):               0.00
Time:                        21:10:18   Log-Likelihood:                 3082.0
No. Observations:                 100   AIC:                            -6160.
Df Residuals:                      98   BIC:                            -6155.
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          9.6562      2e-15   4.83e+15      0.000       9.656       9.656
x1             3.0000   3.45e-16   8.69e+15      0.000       3.000       3.000
==============================================================================
Omnibus:                        4.067   Durbin-Watson:                   0.161
Prob(Omnibus):                  0.131   Jarque-Bera (JB):                4.001
Skew:                           0.446   Prob(JB):                        0.135
Kurtosis:                       2.593   Cond. No.                         11.7
==============================================================================

Lasso回归和岭回归

在线性回归中，有可能出现特征的数量很多，那么模型容易陷入过拟合。为了降低过拟合，这个时候就引入正则项，这种方法叫做正则化。在此之前需要了解下范数的概念。

范数是衡量某个向量空间（或矩阵）中的每个向量以长度或大小。范数的一般化定义：对实数p≥1，范数公式的定义为。这也就引入了常见的L1范数及L2范数。

当p=1时，是L1范数，其表示某个向量中所有元素绝对值的和。

当p=2时，是L2范数，表示某个向量中所有元素平方和再开根，也就是欧几里得距离公式，。

从结果来看，L1范数是向量中各个元素绝对值之和。L2范数是向量各元素平方和然后求平方根。如果损失函数增加L1范数就是提到的Lasso回归，同理损失函数增加L2范数就是岭回归。其实L1范数和L2范数也叫作正则化项。

Lasso 回归和岭回归两种回归均通过在损失函数中引入正则化项来降低过拟合，具体二者和线性回归的损失函数对比如表4.1所示。

回归算法	损失函数（其中称为正则化系数）
线性回归
Lasso回归	$J(\theta ) = \frac{1}{{2n}}\sum\limits_{i = 0}^n {{{({h_0}({x_i}) - {y_i})}^2}} {\rm{ + }}\lambda \sum\limits_{i = 1}^n {\left
岭回归

既然L1和L2正则化都能够达到降低过拟合的目的，那么为什么不结合两者，这就是ElasticNet回归算法的思想。

ElasticNet回归的损失函数：

下面使用Python代码实现Lasso 回归，岭回归和ElasticNet回归。使用的是sklearn中的内置Boston House Price数据集，共有 506 个数据。

Boston House Price数据集房价预测属于是多变量线性回归，具体代码如下。

from sklearn import datasets, linear_model, model_selection
boston = datasets.load_boston()
X_train, X_test, y_train, y_test  = model_selection.train_test_split(boston.data, boston.target, test_size=0.2)

def model(model,X_train, X_test, y_train, y_test):
    #进行训练
    model.fit(X_train, y_train)
    #通过LinearRegression的coef_属性获得权重向量,intercept_获得b的值
    print("权重向量（斜率）:%s, 截距的值为:%.2f" % (model.coef_, model.intercept_))
    #计算出损失函数的值
    print("回归模型的损失函数的值: %.2f" % np.mean((model.predict(X_test) - y_test) ** 2))
    #计算预测性能得分
    print("预测性能得分: %.2f\n" % model.score(X_test, y_test))

    
if __name__ == '__main__':
    print(boston.feature_names)
    print("Losso回归开始训练: ")
    model(linear_model.Lasso(),X_train, X_test, y_train, y_test)
    print("Ridge回归开始训练: ")
    model(linear_model.Ridge(),X_train, X_test, y_train, y_test)
    print("ElasticNet回归开始训练: ")
    model(linear_model.ElasticNet(),X_train, X_test, y_train, y_test)
    print("线性回归开始训练: ")
    model(linear_model.LinearRegression(),X_train, X_test, y_train, y_test)

####输出如下####
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']
Losso回归开始训练: 
权重向量（斜率）:[-0.09864036  0.0603673  -0.          0.         -0.          0.6873437
  0.02190931 -0.75417946  0.28974957 -0.01510544 -0.67198466  0.00691904
 -0.777562  ], 截距的值为:42.42
回归模型的损失函数的值: 22.84
预测性能得分: 0.72

Ridge回归开始训练: 
权重向量（斜率）:[-1.39464324e-01  5.71355155e-02 -6.07057346e-03  2.08884292e+00
 -1.05014171e+01  3.56971544e+00 -5.60264608e-03 -1.50767173e+00
  2.97048802e-01 -1.22397478e-02 -8.22580516e-01  7.36868229e-03
 -5.56814294e-01], 截距的值为:33.56
回归模型的损失函数的值: 16.54
预测性能得分: 0.80

ElasticNet回归开始训练: 
权重向量（斜率）:[-0.11245074  0.06249212 -0.          0.         -0.          0.84657541
  0.02085673 -0.8073735   0.32057332 -0.01616905 -0.70029995  0.00709068
 -0.76506068], 截距的值为:42.17
回归模型的损失函数的值: 22.42
预测性能得分: 0.72

线性回归开始训练: 
权重向量（斜率）:[-1.44187085e-01  5.59860002e-02  2.50465582e-02  2.34282590e+00
 -1.91345074e+01  3.53055150e+00  1.85388413e-03 -1.63915731e+00
  3.17155136e-01 -1.14178760e-02 -9.16285674e-01  6.89942485e-03
 -5.41989771e-01], 截距的值为:39.42
回归模型的损失函数的值: 16.61
预测性能得分: 0.79

回归模型评估

当训练出线性回归模型后，需要对回归模型进行评估，最常用的评价回归模型的指标分别是平均绝对误差，均方误差，决定系数和解释方差。下面依次介绍回归模型评估四大指标。

平均绝对误差

平均绝对误差（Mean Absolute Error，MAE）是所有单个观测值与真实值的偏差的绝对值的平均，其计算公式为，这里的是回归模型的预测值。

均方误差

这里先要了解最小化误差平方和（Sum of Squares for Error，SSE），其计算公式为，SSE计算观测值与真实值的偏差的总平方和，这里的是数据的总数。

均方误差（Mean Squared Error，MSE）是指观测值与真实值之差平方的平均值，其计算公式为，相对于平均绝对误差，MSE越接近0，但是并不能说明模型的性能越好。

决定系数

决定系数（coefficient of determination ，），即判定系数，也称为残差平方和，在机器学习常用r2_sorce表示。

决定系数反映自变量能通过回归关系解释因变量的比例或能力，其计算公式为，这里的指的是真实值的平均值，越接近1，表明变量对的解释能力越强，这个模型对数据拟合的也较好；越接近0，表明模型拟合的越差。

解释方差

解释方差（explained_variance）反映自变量能通过方差解释因变量的比例或者能力，计算公式如下。

下面使用Python代码简单使用回归模型四大指标，具体代码如下。

from sklearn.metrics import mean_absolute_error,mean_squared_error,r2_score,explained_variance_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
print(mean_absolute_error(y_true,y_pred))
print(mean_squared_error(y_true,y_pred))
print(r2_score(y_true,y_pred))
print(explained_variance_score(y_true,y_pred))

####输如下####
0.5
0.375
0.9486081370449679
0.9571734475374732

多项式回归

在很多回归分析中，并不都是线性关系，其中也有可能是非线性关系，如果还使用线性模型去拟合，那么模型的效果就会大打折扣。

比如常见的二次分布，采用的方法就是多项式回归。多项式回归（Polynomial Regression）是研究一个因变量与一个或多个自变量间多项式的回归分析方法。如果自变量只有一个时，称为一元多项式回归；如果自变量有多个时，称为多元多项式回归。

例如，一元m次多项式回归方程为。二元二次多项式回归方程为。

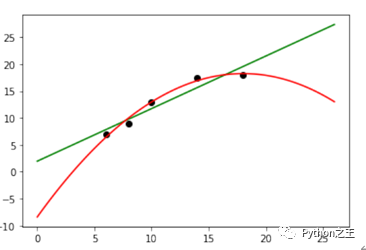
在sklearn使用多项式回归，需要使用sklearn中的PolynomialFeatures生成多项式特征。下面，分别使用线性回归和多项式回归（二次回归）进行线性拟合，具体代码如下。

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt

X_train = [[6], [8], [10], [14], [18]]
y_train = [[7], [9], [13], [17.5], [18]]
X_test = [[6], [8], [11], [16]]
y_test = [[8], [12], [15], [18]]

# 线性回归
model1 = LinearRegression()
model1.fit(X_train, y_train)
xx = np.linspace(0, 26, 100)
yy = model1.predict(xx.reshape(xx.shape[0], 1))
plt.scatter(x=X_train, y=y_train, color='k')
plt.plot(xx, yy, '-g')

# 多项式回归 degree=2 二元二次多项式
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.fit_transform(X_test)
model2 = LinearRegression()
model2.fit(X_train_quadratic, y_train)
xx2 = quadratic_featurizer.transform(xx[:, np.newaxis])
yy2 = model2.predict(xx2)
plt.plot(xx, yy2, '-r')
plt.show()

下面打印线性回归和多线性回归指标，具体代码如下。

print('X_train:\n', X_train)
print('X_train_quadratic:\n', X_train_quadratic)
print('X_test:\n', X_test)
print('X_test_quadratic:\n', X_test_quadratic)
print('线性回归R2：', model1.score(X_test, y_test))
print('二次回归R2：', model2.score(X_test_quadratic, y_test))

####输出如下####
X_train:
 [[6], [8], [10], [14], [18]]
X_train_quadratic:
 [[  1.   6.  36.]
 [  1.   8.  64.]
 [  1.  10. 100.]
 [  1.  14. 196.]
 [  1.  18. 324.]]
X_test:
 [[6], [8], [11], [16]]
X_test_quadratic:
 [[  1.   6.  36.]
 [  1.   8.  64.]
 [  1.  11. 121.]
 [  1.  16. 256.]]
线性回归R2： 0.809726797707665
二次回归R2： 0.8675443656345054