
极市导读
本文详细介绍了两个部分:对数据部分做归一化以及对模型部分做归一化的各类方法,附有详细的公式及代码。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
1. 对数据部分做归一化
主要且常用的归一化操作有BN,LN,IN,GN,示意图如图所示。

图中的蓝色部分,表示需要归一化的部分。其中两维 和 分别表示channel和batch size, 第三维表示 ,, 可以理解为该维度大小是 , 也就是拉长成一维,这样总体就可以用三维图形来表示。可以看出 的计算和batch size相关(蓝色区域为计算均值和方差的单元),而 和 的计算和batch size无关。同时 和 都可以看作是 的特殊情况 是 时候的 是 时候的 。
Batch Normalization;
的简单计算步骤为:
沿着通道计算每个batch的均值 。 沿着通道计算每个batch的方差 。 对x做归一化, 加入缩放和平移变量 和 ,归一化后的值,
适用于判别模型中,比如图片分类模型。因为 注重对每个batch进行归一化,从而保证数据分布的 一致性,而判别模型的结果正是取决于数据整体分布。但是 对batchsize的大小比较敏感,由于每次计 算均值和方差是在一个batch上,所以如果batchsize太小,则计算的均值、方差不足以代表整个数据分布。 (其代码见下BN的前向与反向的代码详解!)
在训练过程之中,我们主要是通过滑动平均这种Trick的手段来控制变量更新的速度。
`def batchnorm_forward(x, gamma, beta, bn_param):"""Input:- x: (N, D)维输入数据- gamma: (D,)维尺度变化参数- beta: (D,)维尺度变化参数- bn_param: Dictionary with the following keys:- mode: 'train' 或者 'test'- eps: 一般取1e-8~1e-4- momentum: 计算均值、方差的更新参数- running_mean: (D,)动态变化array存储训练集的均值- running_var:(D,)动态变化array存储训练集的方差Returns a tuple of:- out: 输出y_i(N,D)维- cache: 存储反向传播所需数据"""mode = bn_param['mode']eps = bn_param.get('eps', 1e-5)momentum = bn_param.get('momentum', 0.9)N, D = x.shape# 动态变量,存储训练集的均值方差running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))out, cache = None, None# TRAIN 对每个batch操作if mode == 'train':sample_mean = np.mean(x, axis = 0)sample_var = np.var(x, axis = 0)x_hat = (x - sample_mean) / np.sqrt(sample_var + eps)out = gamma * x_hat + betacache = (x, gamma, beta, x_hat, sample_mean, sample_var, eps)#滑动平均(影子变量)这种Trick的引入,目的是为了控制变量更新的速度,防止变量的突然变化对变量的整体影响,这能提高模型的鲁棒性。running_mean = momentum * running_mean + (1 - momentum) * sample_meanrunning_var = momentum * running_var + (1 - momentum) * sample_var# TEST:要用整个训练集的均值、方差elif mode == 'test':x_hat = (x - running_mean) / np.sqrt(running_var + eps)out = gamma * x_hat + betaelse:raise ValueError('Invalid forward batchnorm mode "%s"' % mode)bn_param['running_mean'] = running_meanbn_param['running_var'] = running_varreturn out, cache`
对于BN的反向传播,首先来推导下公式,这里先定义下一些参数变量:
是一个batch中所有样本的方差。 是一个batch中所有样本的均值。 为归一化后的样本数据。 为输入样本 经过尺度变化后的输出。 与$为尺度变化系数。 是上一层的梯度,并且假设 都是 维。即有 个维度为 的样本,在 的前向传播中 通 过 将 变换为 那么反向传播是根据 求得 求解
求解
求解 根据论文的公式和链式法则可得下面的等式: 我们这里又可 以先求 有了 ,就可以求出
下面来一个背诵版本:
因此,的反向传播代码如下:
`def batchnorm_backward(dout, cache):"""Inputs:- dout: 上一层的梯度,维度(N, D),即 dL/dy- cache: 所需的中间变量,来自于前向传播Returns a tuple of:- dx: (N, D)维的 dL/dx- dgamma: (D,)维的dL/dgamma- dbeta: (D,)维的dL/dbeta"""x, gamma, beta, x_hat, sample_mean, sample_var, eps = cacheN = x.shape[0]dgamma = np.sum(dout * x_hat, axis = 0)dbeta = np.sum(dout, axis = 0)dx_hat = dout * gammadsigma = -0.5 * np.sum(dx_hat * (x - sample_mean), axis=0) * np.power(sample_var + eps, -1.5)dmu = -np.sum(dx_hat / np.sqrt(sample_var + eps), axis=0) - 2 * dsigma*np.sum(x-sample_mean, axis=0)/ Ndx = dx_hat /np.sqrt(sample_var + eps) + 2.0 * dsigma * (x - sample_mean) / N + dmu / Nreturn dx, dgamma, dbeta`
那么为啥要用 呢? 的作用如下:
加快网络的训练与收敛的速度
在深度神经网络中中,如果每层的数据分布都不一样的话,将会导致网络非常难收敛和训练。如果把每层的数据都在转换在均值为零,方差为1 的状态下,这样每层数据的分布都是一样的训练会比较容易收敛。
控制梯度爆炸防止梯度消失
以 函数为例,函数使得输出在 之间,实际上当 输入过大或者过小,经过sigmoid函数后输出范围就会变得很小,而且反向传播时的梯度也会非常小,从而导致梯度消失,同时也会导致网络学习速率过慢; 同时由于网络的前端比后端求梯度需要进行更多次的求导运算,最终会出现网络后端一直学习,而前端几乎不学习的情况。Batch Normalization (BN) 通常被添加在每一个全连接和激励函数之间,使数据在进入激活函数之前集中分布在0值附近,大部分激活函数输入在0周围时输出会有加大变化。
同样,使用了 之后,可以使得权值不会很大,不会有梯度爆炸的问题。
防止过拟合
在网络的训练中,BN的使用使得一个中所有样本都被关联在了一起,因此网络不会从某一个训练样本中生成确定的结果,即同样一个样本的输出不再仅仅取决于样本的本身,也取决于跟这个样本同属一个的其他样本,而每次网络都是随机取,比较多样,可以在一定程度上避免了过拟合。
Instance Normalization
IN适用于生成模型中,比如图片风格迁移。因为图片生成的结果主要依赖于某个图像实例,所以对整个归一化不适合图像风格化中,在风格迁移中使用 。不仅可以加速模型收敛,并且可以保持每个图像实例之间的独立。
当然,其前向反向的推导与相似,无非是维度的问题了~
代码如下所示:
def Instancenorm(x, gamma, beta):# x_shape:[B, C, H, W]results = 0.eps = 1e-5x_mean = np.mean(x, axis=(2, 3), keepdims=True)x_var = np.var(x, axis=(2, 3), keepdims=True0)x_normalized = (x - x_mean) / np.sqrt(x_var + eps)results = gamma * x_normalized + betareturn results
Layer Normalization
是指对同一张图片的同一层的所有通道进行操作。与上面的计算方式相似,计算均值与方差,在计算缩放和平移变量 和 。 主要用在 任务中, 当然, 像中存在的就是
def Layernorm(x, gamma, beta):# x_shape:[B, C, H, W]results = 0.eps = 1e-5x_mean = np.mean(x, axis=(1, 2, 3), keepdims=True)x_var = np.var(x, axis=(1, 2, 3), keepdims=True0)x_normalized = (x - x_mean) / np.sqrt(x_var + eps)results = gamma * x_normalized + betareturn results
为什么RNN中不使用BN?
可以展开成一个隐藏层共享参数的 , 随着时间片的增多,展开后的 的层 数也在增多,最终层数由输入数据的时间片的数量决定,所以 是一个动态的网络。在 网络中, 一个的数据中,通常各个样本的长度都是不同的。往往在最后时刻,只有少量样本有数据,基于这个样本的统计信息不能反映全局分布,所以这时 的效果并不好。
而当将 添加到 之后,实验结果发现 破坏了卷积学习到的特征,模型无法收敛,所以在 之后使用 是一个更好的选择。
对于 与 而言, 取的是不同样本的同一个特征, 而 取的是同一个样本的不同特征。在 和 都能使用的场景中, 的效果一般优于 , 原因是基于不同数据,同一特征得到的归一化特征更不容易损失信息。但是有些场景是不能使用 的,例如较小或者在中,这时候可以选择使用 , 得到的模型更稳定且起到正则化的作用。 能应用到小批量和 中是因为 的归一化统计量的计算是和没有关系的。
Group Normalization
是针对 (BN) 在较小时错误率较高而提出的改进算法, 因为 层的计算结果依赖当前batch的数据,当batchsize较小时 (比如2 、 4这样) , 该数据的均值和方差的代表性较差, 因此对最后的结果影响也较大。
其中, 是将通道数 分成G份,每份 , 当 时,每份G个,所以为一整块的,即为 。当 时,每份只有1个,所以为 。
是指对同一张图片的同一层的某几个 不是全部) 通道一起进行Normalization操作。这几个通道称为一个。计算相应的均值以及方差,计算缩放和平移变量 和 其代码如下所示:
def GroupNorm(x, gamma, beta, G=16):# x_shape:[B, C, H, W]# gamma, beta, scale, offset : [1, c, 1, 1]# G: num of groups for GNresults = 0.eps = 1e-5x = np.reshape(x, (x.shape[0], G, x.shape[1]/16, x.shape[2], x.shape[3]))x_mean = np.mean(x, axis=(2, 3, 4), keepdims=True)x_var = np.var(x, axis=(2, 3, 4), keepdims=True0)x_normalized = (x - x_mean) / np.sqrt(x_var + eps)results = gamma * x_normalized + betareturn results
Switchable Normalization
中表明了一个观点:层的成功和协方差什么的没有关联!证明这种层输入分布稳定性与的成功几乎没有关系。相反,实验发现会对训练过程产生更重要的影响:它使优化解空间更加平滑了。这种平滑使梯度更具可预测性和稳定性,从而使训练过程更快。
的具体做法可以从图中看出来:
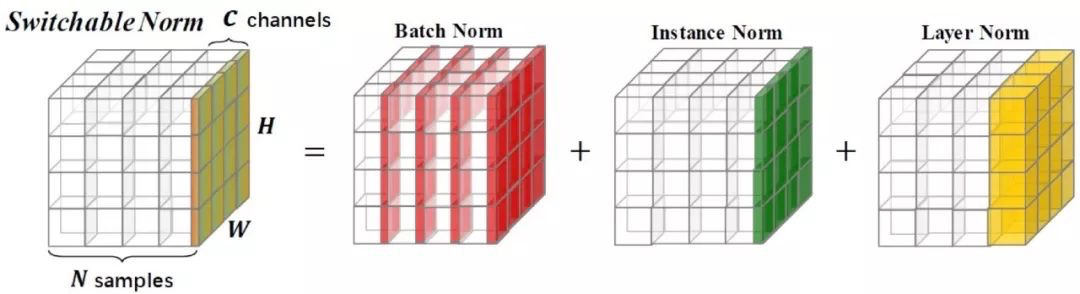
论文中认为:
第一,归一化虽然提高模型泛化能力,然而归一化层的操作是人工设计的。在实际应用中,解决不同的问题原则上需要设计不同的归一化操作,并没有一个通用的归一化方法能够解决所有应用问题; 第二,一个深度神经网络往往包含几十个归一化层,通常这些归一化层都使用同样的归一化操作,因为手工为每一个归一化层设计操作需要进行大量的实验。
而与强化学习不同,使用可微分学习,为一个深度网络中的每一个归一化层确定合适的归一化操作。
算法是为三组不同的 以及 分别学习三个总共6个标量值 和 表示 一个输入维度为 的特征图, 为归一化之后的特征图。
其中 。在计算 和 时,我们可以使用 作为 中间变量以减少计算量。
是通过softmax计算得到的激活函数: and
其中 是需要优化的3个参数,可以通过BP调整它们的值。同理我们也可以计算 对应的参数值 从上面的分析中我们可以看出, SN只增加了6个参 数 假设 原始网络的参数集为 , 带有SN的网络的损失 函数可以表示为 , 他可以通过BP联合 优化 和
代码如下:
def SwitchableNorm(x, gamma, beta, w_mean, w_var):# x_shape:[B, C, H, W]results = 0.eps = 1e-5mean_in = np.mean(x, axis=(2, 3), keepdims=True)var_in = np.var(x, axis=(2, 3), keepdims=True)mean_ln = np.mean(x, axis=(1, 2, 3), keepdims=True)var_ln = np.var(x, axis=(1, 2, 3), keepdims=True)mean_bn = np.mean(x, axis=(0, 2, 3), keepdims=True)var_bn = np.var(x, axis=(0, 2, 3), keepdims=True)mean = w_mean[0] * mean_in + w_mean[1] * mean_ln + w_mean[2] * mean_bnvar = w_var[0] * var_in + w_var[1] * var_ln + w_var[2] * var_bnx_normalized = (x - mean) / np.sqrt(var + eps)results = gamma * x_normalized + betareturn results
值得一提的是在测试的时候,在 的 部分,它使用的是一种叫做批平均 (batch
average)的方法,它分成两步:1.固定网络中的 层, 从训练集中随机抽取若干个批量的
样本,将输入输入到网络中; 2.计算这些批量在特定SN层的 和 的平均值,它们将会作为测试阶段的均值和方差。实验结果表明, 在 中批平均的效果略微优于滑动平均。
当然,还有一些基于数据的归一化,如IBN、BIN等,都是相似的做法!
2. 对模型权重做归一化
Weight Normalization
是在权值的维度上做的归一化。 做法是将权值向量 在其欧氏范数和其方向上解塊成了参数向量 和参数标量 后使用 分别优化这两个参数。
也是和样本量无关的, 所以可以应用在较小以及 等动态网络中; 另外 使用的基于 的归一化统计量代替全局统计量,相当于在梯度计算中引入 了噪声 。而 则没有这个问题, 所以在生成模型与强化学习等噪声敏感的环境中 的 效果也要优于 。
的计算过程:
对于神经网络而言,一个节点的计算过程可以表达为:
其中 是与该神经元连接的权重,通过损失函数与梯度下降对网络进行优化的过程就是求解最优 的过程。将 的长度与方向解塊,可以将 表示为:
为与该神经元连接的权重,通过损失函数与梯度下降对网络进行优化 的过程就是求解最优 的 过程。将 的长度与方向解塊,可以将 表示为
其中 为标量,其大小等于 的模长, 为与 同方向的单位向量,此时,原先训练过 程 中 的学习转化为 和 的学习。假设损失函数以 表示,则 对 和 的梯度可 以分别 表示为,
因为
所以
其中 , 与向量点乘可以投影任意向量至 的补空间。相对于原先的 进行了 的缩放与 的投影。这两者都对优化过程起到作用。
对于 而言, , 因为 , 所以 与 正交。
假设, , 则 可以影响 模长的增长,同时 的模长也影响 的大小。
因此,我们可以得到:
表明 会对权重梯度进行 的缩放。 表明WN会将梯度投影到一个远离于 的方向。
代码可以参考:
import torch.nn as nnimport torch.nn.functional as F# 以一个简单的单隐层的网络为例class Model(nn.Module):def init(self, input_dim, output_dim, hidden_size):super(Model, self).init()# weight_normself.dense1 = nn.utils.weight_norm(nn.Linear(input_dim, hidden_size))self.dense2 = nn.utils.weight_norm(nn.Linear(hidden_size, output_dim))def forward(self, x):x = self.dense1(x)x = F.leaky_relu(x)x = self.dense2(x)return x
Spectral Normalization
首先看下这个图,了解下一个数学概念叫做Lipschitz 连续性:
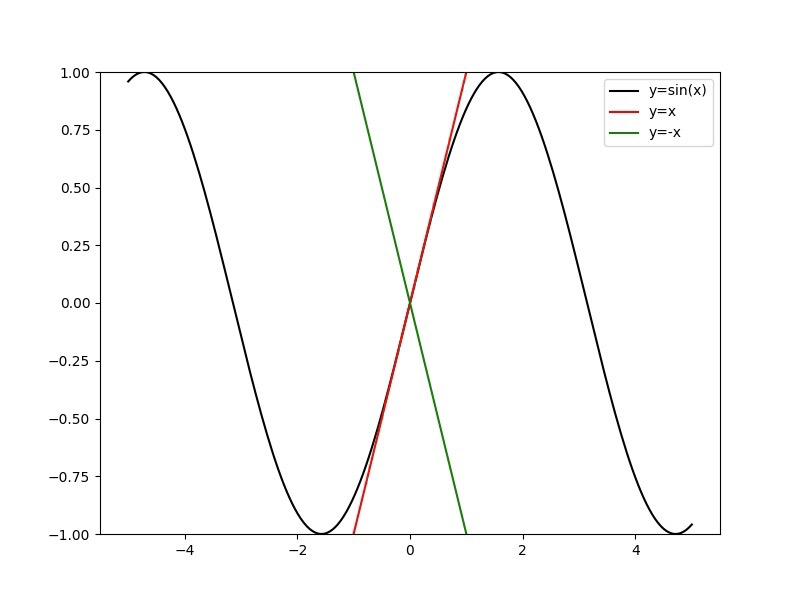
Lipschitz 条件限制了函数变化的剧烈程度, 即函数的梯度。在一维空间中,很容易看出 是1 Lipschitz的,它的最大斜率是 1 。
如 与 的斜率是1与 求导是 , 值域为
在GAN中,假设我们有一个判别器 , 其中 是图像空间。如果判别器是 Lipschitzcontinuous 的, 那么对图像空间中的任意 和 , 有:
其中 为 norm,如果 取到最小值, 那么 被称为
首先抛出结论:
矩阵 除以它的 spectral norm 可以使其具有 Lipschitz continuity.
那么Spectral Normalization的具体做法如下:
将神经网络的每一层的参数 作 分解,然后将其最大的奇异值限定为1, 满足 Lipschitz条件。
在每一次更新 之后都除以 最大的奇异值。这样,每一层对输入 最大的拉伸系数不会超过 1 。
经过 Spectral 之后,神经网络的每一层 权重,都满足
对于整个神经网络 自然也就满足利普希茨连续性了
在每一次训练迭代中,都对网络中的每一层都进行 分解,是不现实的,尤其是当网络权重维度很大的时候。我们现在可以使用一种叫做power teration的算法。
Power iteration 是用来近似计算矩阵最大的特征值(dominant eigenvalue 主特征值)和其对应的特征向量(主特征向量)的。
假设矩阵 是一个 的满秩的方阵,它的单位特征向量为 , 对于的特征值为 那么任意向量 。则有:
我们通过k次迭代
由于 (不考虑两个特征值相等的情况,这种情况比较少见!) 。可知,经过 次迭代后,则:
也因此:
也就是说,经过 次迭代后,我们将得到矩阵主特征向量的线性放缩,只要把这个向量归一化,就得到了该矩阵的单位主特征向量,进而可以解出矩阵的主特征值。
而我们在神经网络中,想求的是权重矩阵 的最大奇异值,根据上面几节的推导,知道这个奇异值正是最大特征值的开方。因此,我们可以采用 的方式求解的单位主特征向量,进而求出最大特征值。论文中给出的算法是这样的:
那么,当知道单位主特征向量之后,如何求出最大的特征值。
同样,我们可以得到:
具体的代码实现过程中,可以随机初始化一个噪声向量代入公式 (13)。由于每次更新参数的很小,矩阵 的参数变化都很小,矩阵可以长时间维持不变。
因此,可以把参数更新的 和求矩阵最大奇异值的 融合在一起,即每更新一次权 重 , 更新一次和, 并将矩阵归一化一次。
代码如下:
import torchfrom torch.optim.optimizer import Optimizer, requiredimport torch.nn.functional as Ffrom torch import nnfrom torch import Tensorfrom torch.nn import Parameterdef l2normalize(v, eps=1e-12):return v / (v.norm() + eps)class SpectralNorm(nn.Module):def init(self, module, name='weight', power_iterations=1):super(SpectralNorm, self).init()self.module = moduleself.name = nameself.power_iterations = power_iterationsif not self._made_params():self._make_params()def _update_u_v(self):u = getattr(self.module, self.name + "_u")v = getattr(self.module, self.name + "_v")w = getattr(self.module, self.name + "_bar")height = w.data.shape[0]for _ in range(self.power_iterations):v.data = l2normalize(torch.mv(torch.t(w.view(height,-1).data), u.data))u.data = l2normalize(torch.mv(w.view(height,-1).data, v.data))# sigma = torch.dot(u.data, torch.mv(w.view(height,-1).data, v.data))sigma = u.dot(w.view(height, -1).mv(v))setattr(self.module, self.name, w / sigma.expand_as(w))def _made_params(self):try:u = getattr(self.module, self.name + "_u")v = getattr(self.module, self.name + "_v")w = getattr(self.module, self.name + "_bar")return Trueexcept AttributeError:return Falsedef _make_params(self):w = getattr(self.module, self.name)height = w.data.shape[0]width = w.view(height, -1).data.shape[1]u = Parameter(w.data.new(height).normal_(0, 1), requires_grad=False)v = Parameter(w.data.new(width).normal_(0, 1), requires_grad=False)u.data = l2normalize(u.data)v.data = l2normalize(v.data)w_bar = Parameter(w.data)del self.module._parameters[self.name]self.module.register_parameter(self.name + "_u", u)self.module.register_parameter(self.name + "_v", v)self.module.register_parameter(self.name + "_bar", w_bar)def forward(self, *args):self._update_u_v()return self.module.forward(*args)
引用
[1]https://www.zhihu.com/question/326034346/answer/730051338
[2]https://zhuanlan.zhihu.com/p/54530247
[3]https://zhuanlan.zhihu.com/p/57807576
[4]https://blog.csdn.net/u014380165/article/details/79810040
如果觉得有用,就请分享到朋友圈吧!
公众号后台回复“异常检测”获取异常检测综述资源~
极市干货
深度学习环境搭建:个人深度学习工作站配置指南|深度学习主机配置推荐
实操教程:用OpenCV的DNN模块部署YOLOv5目标检测|TensorRT的FP16模型转换教程
算法技巧(trick):17种提高PyTorch“炼丹”速度方法|PyTorch Trick集锦|深度学习调参tricks总结
最新CV竞赛:2021 高通人工智能应用创新大赛|CVPR 2021 | Short-video Face Parsing Challenge


# CV技术社群邀请函 #

备注:姓名-学校/公司-研究方向-城市(如:小极-北大-目标检测-深圳)
即可申请加入极市目标检测/图像分割/工业检测/人脸/医学影像/3D/SLAM/自动驾驶/超分辨率/姿态估计/ReID/GAN/图像增强/OCR/视频理解等技术交流群
每月大咖直播分享、真实项目需求对接、求职内推、算法竞赛、干货资讯汇总、与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度等名校名企视觉开发者互动交流~






