1引言

首先，题目中的三个概念对应三类空间，即度量空间（Metric space）、赋范空间（Normed space）和内积空间（Inner prodect space）。

度量空间，赋范空间，内积空间

从下图可以看到，这些空间底层都是集合，而所谓拓扑空间（Topological space）就是一个集合  与定义在其上的一个拓扑结构 组成的二元组 。

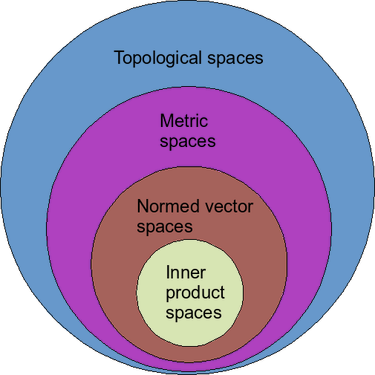
如果光是个集合，里面的元素孤零零的，干不了什么事情呀。定义了拓扑结构，给元素间建立了一定关系，那么大家可以相互打交道，可以开心地搞事情了嘛。不同的结构意味着不同的关系，也意味着能搞不同的事情。而这时的集合就升级为空间了。

度量空间、赋范空间以及内积空间，都是通常称为拓扑空间的示例。这些空间是按照结构递增的顺序给出的。也就是说，每个内积空间都是赋范空间，而每个赋范空间又都是度量空间。这里，度量空间相对来说是最容易构建的，但由于增加了更多结构，内积空间使用起来更加有用。

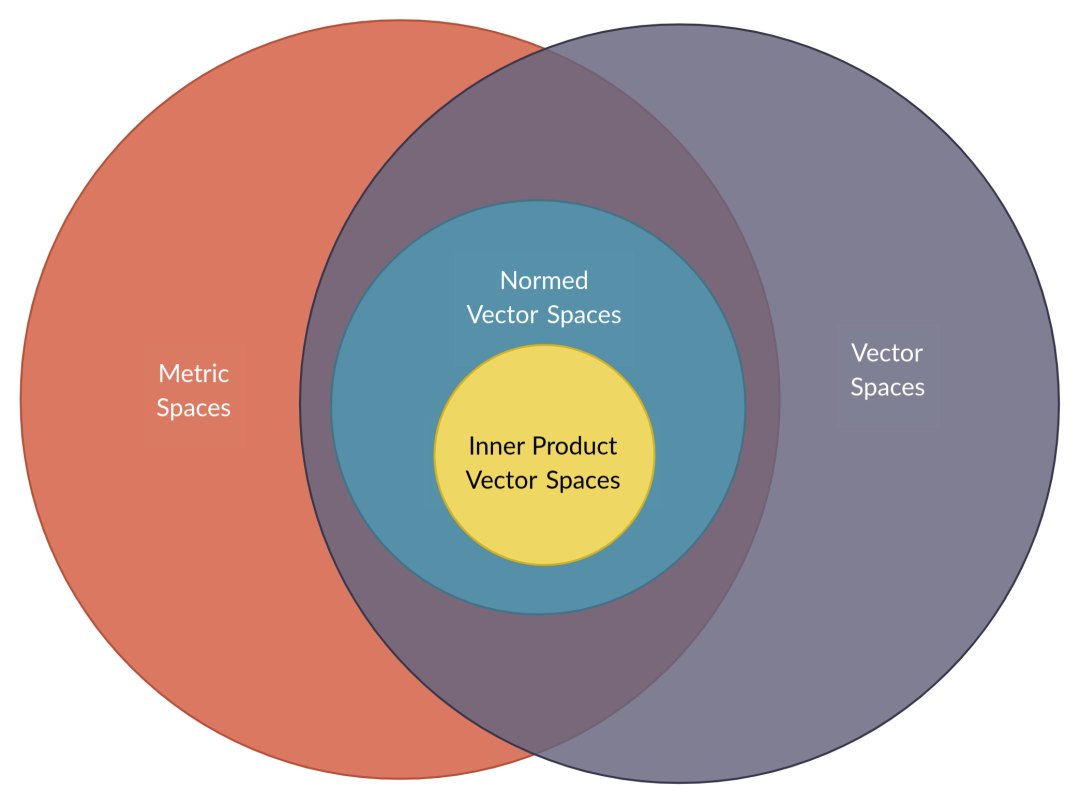
度量空间与其他两类空间，即赋范空间和内积空间在一定角度上是有区别的，后面两类空间也是线性空间（向量空间）的特例。

度量空间、向量空间、赋范空间以及内积空间这四者之间的关系可以用下面的文氏图简单概括起来。

这几个空间的来历大致如下，

• 意大利数学家朱塞佩·皮亚诺（Giuseppe Peano）在 1888 年首次给出向量空间的公理化定义。

• 法国数学家弗雷歇（Fréchet）在 1906 年提出了抽象度量空间的一般概念。

• 波兰数学家巴拿赫（Banach）在 1922 年提出了赋范空间的公理化定义。

• 匈牙利数学家（后移民美国）冯·诺依曼（John von Neumann）在 1930 年左右提出内积空间的公理化定义。

实际上，上面这些概念的起源以及公理化定义，都可以在他们前辈的作品中窥见到。比如像内积，皮亚诺早在 1898 年的论文中就已经引入。

在数学中，很多事情往往并不是孤立事件，承前启后是常见的事情。可见，数学家之间也是存在结构的。

2度量空间

度量是指测量空间中点之间的距离的一种方式。例如，空间 是具有如下度量的度量空间

该度量用于计算 中点 和点 之间的距离。该度量是 上的欧几里德标准度量。

通常，度量空间 是一个集合 配上一个函数 ，而该函数就是所谓的度量，它必须满足以下四个条件：

（i）对于所有 ，有 。（非负性）

（ii） 当且仅当 。（非退化性）

（iii）对于所有 ，有 。（对称性）

（iv）对于所有 ，有 。（三角不等式）

简蛋来说，上面几点分别对应下面几个特性，

• 任两点间的距离为正数

• 每个点只有和自己的距离为 0

• 从 到 的距离，等同于从 到 的距离

• 从 到 的距离小于等于从 先经过 再到 的距离

度量空间主要是从点之间的距离这个角度对欧几里德空间 作了推广。从常见的距离概念里提取一些重要性质，将它们保留下来作为定义距离的条件。换句话说，只要满足这些条件就有资格成为距离，而有了距离的概念，可以将欧几里德空间里的一些拓扑性质移植到度量空间中。

除了 ，还有哪些度量空间的示例？

例 1. 令 为复数集，定义度量 。

例 2. 令 为任意一个集合并定义

这称为离散度量。

中的许多拓扑概念都可以扩展到更一般的度量空间上。例如，如果对于每个正数 ，都存在一个正整数 ，只要当 时 均成立，则称度量空间 中的序列 收敛到元素 。

3向量空间

向量简史

我们先简单地来看一下向量（vector）的简历。

vector 或 vecteur 源自拉丁语动词的过去分词 vectus，意为携带或运输。最早可能被天文学家引入，用于描述行星围绕恒星构成向量半径。

虽然向量（vector）的名称早在十八世纪就有人使用，但在数学上将向量作为有向线段的想法可以说源于莫比乌斯（Mobius，1827）和格拉斯曼（Grassmann，1844），以及提出四元数的汉密尔顿（Hamilton，1845），他将其用于区分四元数中所谓的向量部分和标量部分。

接着，格拉斯曼和汉密尔顿的两大体系相互竞争，争夺影响力。从 1840 年代到 1870 年代，哈密顿体系在欧洲大部分地区比格拉斯曼体系发展得好得多。从 1870 年代到 1890 年代，关于格拉斯曼体系的出版物数量大大增加，提出向量空间公理化定义的皮亚诺（Peano，1888）就是属于这一波。

在那个年代，还没有像今天这样使用点来表示向量。向量的概念通常被视为有向线段 或两个点 和 的差 。物理学家将向量视为兼具方向和大小的量（例如动量或力）。作为有向线段，当两个向量具有相同的长度和相同的方向时，它们被认为是相等的。

通常认为向量最多具有三个维度，而在格拉斯曼体系中，向量被允许具有任意数量的维数。向量的更一般概念，抽象向量空间，一开始是在皮亚诺的工作中以线性系统的名称出现的。

向量空间

皮亚诺在其职业生涯的不同时期以三种不同的方式对待类似向量的概念。

• 从 1887 年开始的第一种方式是 -元组，向量加法以及标量-向量乘法由每个坐标上的相应运算定义。他并没有将这些 -元组看成向量。

• 从 1888 年开始的第二种方式是将两点 和 的差 看成有向线段。

• 第三种方式也是从 1888 年开始的，他称之为线性系统（现在称为向量空间）。

第一种方式并没有公理化，第二种方式在十年后，即 1898 年被皮亚诺公理化。那会儿他不再使用线性系统这第三种方式子了。再过了十多年，有学者开始采用他的公理化线性系统才使之被学术界熟知。

下面我们来看看向量空间的现代版公理化定义。

向量空间的公理化定义

给定域 ， 上的向量空间 是一个集合，其上定义了两种二元运算，

• 向量加法 ，把 中的两个元素 和 映射到 中另一个元 素，记作 。

• 标量乘法 ，把 中的一个元素 和 中的一个元素 变为 中 的另一个元素，记作 。

中的元素称为向量，而 中的元素称为标量。而集合 才构成一个向量空间（对 中的任意元素 、 以及 中的任意元素 都成立）。

前四个公理说明配备了向量加法的 是一个交换群，后面四个公理主要针对标量-向量乘法。这里，向量之间的加法 + 和标量之间的加法 + 是不同的，标量与向量之间的标量乘法 · 和两个标量之间的乘法（域 中自带的乘法）也是不同的。

向量空间的一个直观模型是向量几何，几何上的向量及相关的运算即向量加法，标量乘法，以及对运算的一些限制如封闭性，结合律，已大致地描述了向量空间这个数学概念的直观形象。

有了公理化定义后，现在的向量空间不光是指几何上的向量了，是抽象的向量了。但是，人们往往需要对向量空间中的抽象向量作进一步分析，因此需要引入向量的长度，向量间的角度以及向量的正交性等概念。

赋范空间

线性代数中的很多概念在一定意义上可以说是源自几何，因为许多主题是出于将 和 中的基本几何概念推广到高维空间的目的而发展而来的。通常的方法是从 和 中的几何概念出发，然后将有关有序对和三元组的概念扩展为 和 中的有序 元组。

例如，通过计算直角三角形的斜边的长度，可以从勾股定理中获得向量 或 的长度，如下图所示。

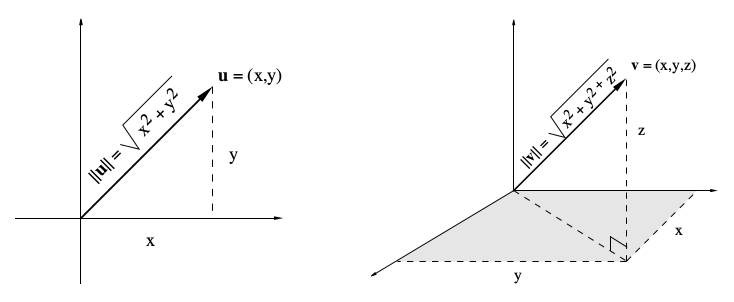
这里，长度的计算公式为，

在 和 中被称为欧几里得范数，这种方式很显然可以推广到高维空间。

一个实赋范向量空间 是一个实数域向量空间 配上一个被称为范数的函数 。这个函数满足四个条件，

-（i）对于所有 ，有 。（非负性）

-（ii） 当且仅当 。（非退化性）

-（iii）对于所有 和 ，有 。（齐性）

-（iv）对于所有向量 ，成立关系式 。（三角不等式）

现在，我们给出几个基本的赋范向量空间。

例 1. ，配上范数 。

例 2. ，参考低维的情况，给它配上范数 。

这是 上的标准欧几里得范数，通常用 表示。

例 3. ，配上范数 。

p-范数

对于 ， 的 -范数定义为

实际上，常用下面三个 -范数，

• 1-范数

• 2-范数（欧几里得范数）

• 无穷大范数

例如，，那么 ，，以及 。

度量和范数的关系

就度量和范数之间的关系来说，范数总是可以引出度量。具体来说，如果 是一个赋范空间，那么可以如下定义函数

那么， 就是 上的一个度量。

但是，反过来则不一定成立的，即并非所有度量都可以由某个范数来定义。

例如，离散度量不能用范数定义。这是因为对于任一个范数，当 时有 。因此，当 时有 。然而，除去 时，离散度量 。

范数的公理化定义中有齐性这条，而度量的定义里面并没有这条。某种意义上说，度量的条件是比范数的条件要来的低，因此能成为范数，必然能被拿来打造度量，而反过来就不一定了。

如果考虑在 上的三个范数 ， 和 ，则只有中间的那个会引出对 上的标准度量。另外两个范数会导出其他度量。例如，由第一个范数定义的度量为

内积空间

内积空间的想法是推广一种欧几里得空间具有的理想特性从而得到一种抽象结构，在此基础上可以计算距离以及确定抽象向量间的正交性和角度。

一个实数域上的内积空间 是实向量空间配上一个称为内积的函数 ，这个函数满足以下五个条件，

• i、所有 ，有 。（非负性）

• ii、 当且仅当 时。（非退化性）

• iii、对于所有向量  以及实数 ，有 成立。（齐性）

• iv、对于  有 。（对称性）

• v、对于所有向量 ，都有 。（分配律）

在上面定义中，如果将 替换为 ，则相应的对称性替换为 Hermitian 对称性

对于所有向量 ，其中的横杠表示复共轭。这样，我们得到一个复内积空间。

下面是两个基本的内积空间示例。

例1. 实线性空间 配上标准内积，

例2. 复线性空间 配上标准内积

内积与范数、度量的关系

首先，内积总是可以导出范数。具体来说，如果 是内积空间，而 由如下定义，

那么 是 上的范数。然后，利用范数与度量之间的关系，内积也可以进一步导出度量。

由于每个内积都可以根据公式 导出范数，因此很自然地要问相反的情况是否也成立呢？

也就是说，对于空间 上的每个向量范数 ，是否存在 上相应的内积 ，使得 成立？

如果答案是否定的，那么在什么条件下，内积会生成给定的范数？

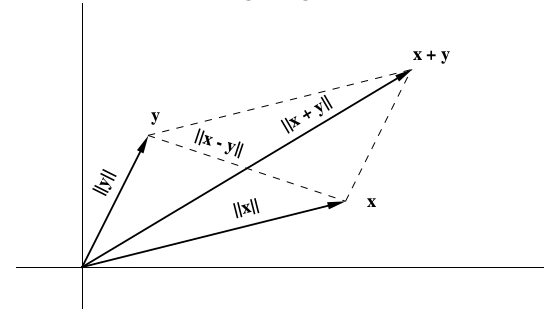
平行四边形恒等式

对于向量空间 上的给定范数 ，在 上存在一个内积，使得 当且仅当如下平行四边形恒等式

对于所有 上的 和 均成立。该恒等式表示平行四边形的对角线长度的平方之和是其边长的平方和的两倍。这里的意思就是，如果一个范数满足平行四边形恒等式，那么它可以由一个内积定义。换句话说，平行四边形恒等式表征了那些由内积产生的范数。

我们已经知道 上的欧几里得向量范数是由标准内积生成的，因此上面的定理保证了平行四边形恒等式对于 2-范数必须是成立的。

通过观察可以很容易地证实这一点

之所以如此命名平行四边形，是因为它表示一个事实，即平行四边形中对角线的平方和是侧边平方和的两倍，请参见下图。

另外，内积与范数还能一起搞事情，那就是所谓的 CBS（Cauchy-Bunyakovskii-Schwarz）不等式。

如果 是一个内积空间，则对于所有 有

把右边的内积写成范数，可以改成下面这样子。

如果 是一个内积空间，并且令 ，则对于 上所有 和 ，有

当且仅当 ，其中 时，等式成立。

内积与向量正交

另外，内积为我们提供了一种讨论所谓正交性的方式。

众所周知，如果 中的两个向量之间的角度为直角，即 ，则它们是垂直的。

但是直角的视觉概念在更高维空间中并不可用，因此我们必须从本质上挖掘关于垂直更深层的含义。

换句话说，所谓垂直，除了角度是 外，还能反映在别的量上面吗？

还真的有，不从角度来看，而是从三角形的边长上来看，也能导出垂直的概念。

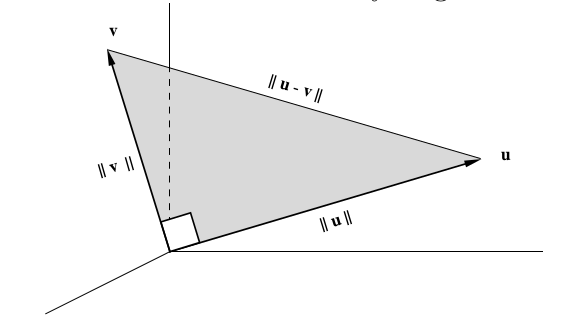
回想一下小时候学的数学知识，即经典的毕达哥拉斯定理（Pythagorean theorem），当然，我们称它为勾股定理。利用该定理，从边长上可以发现  和 中的垂直性的本质。

而边长不就对应了向量的范数吗！

那么，我们就用范数的语言来书写该定理，得到: 当且仅当

成立时， 和 是垂直（正交）的。

如下图所示，只要计算一下相关的三个向量的范数，就能知道两个向量是否垂直了。

进一步，对所有 都使用 ，以及 。因此，我们可以将勾股定理重写为

当且仅当 时， 和 是 中的正交向量。由它作扩展，我们自然而然能得到在更一般空间上的正交概念的定义。

在内积空间 中，当 时，两个向量 ， 被称为相互正交，记为 。

• 对于带有标准内积的 ，有

• 对于带有标准内积的 ，有